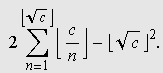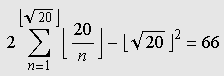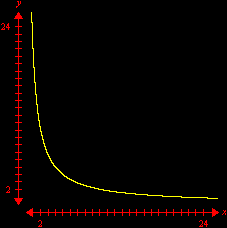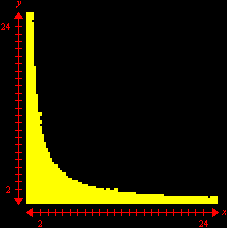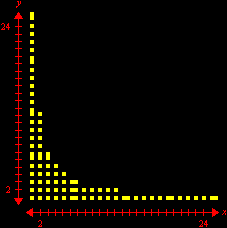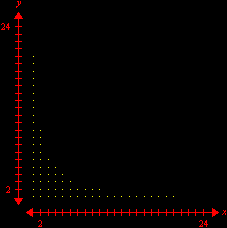
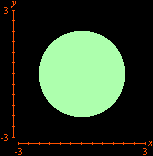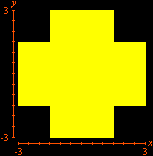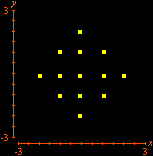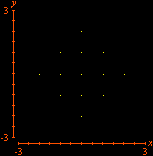
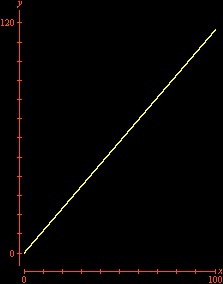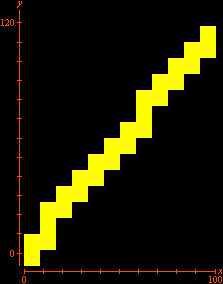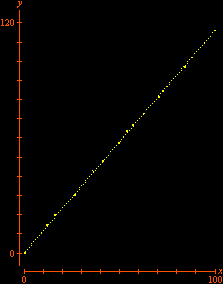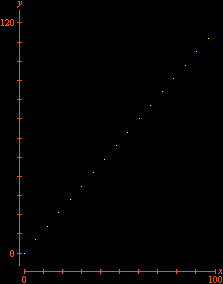
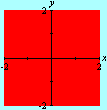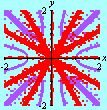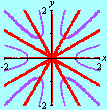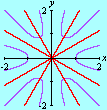
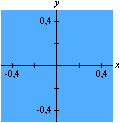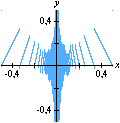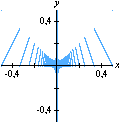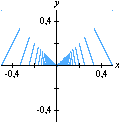
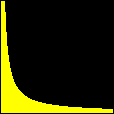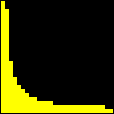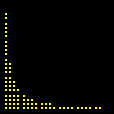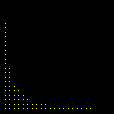
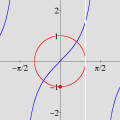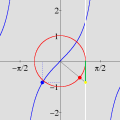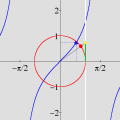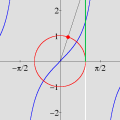
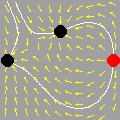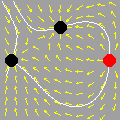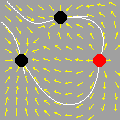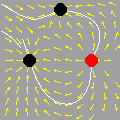
Pontos com Coordenadas Inteiras Outros exemplos (versão em inglês) Prepare-se para mais uma seção de Matemática laboratorial com o incrível GrafEq. Pela primeira vez em toda a Internet, você verá como esse software pode contar pontos com coordenadas inteiras em certos conjuntos do plano cartesiano. Um belo e instrutivo exemplo é o que resulta da contagem de tais pontos abaixo de uma hipérbole. É intuitivamente óbvio que a região do primeiro quadrante abaixo de uma hipérbole , , incluindo a hipérbole mas excluindo os eixos, possui um número finito de pontos com coordenadas inteiras. Muito menos óbvio é que se pode utilizar a função piso (ou "máximo inteiro") para mostrar que esse número é dado por Exercício 1. Prove esse resultado. O leitor que enviar o argumento mais convincente será premiado com uma publicação neste site. Podemos testar essa fórmula no GrafEq atribuindo valores a c. Por exemplo, a expressão nos diz que há pontos contidos na região definida pelas inequações . O GrafEq sabe lidar com sistemas de equações e inequações em notação tradicional, de modo que torna-se fácil entrar com essas informações, uma a uma, e autorizar o processamento. Armado com a sua espetacular técnica de refinamentos sucessivos, o GrafEq efetua uma espécie de varredura recursiva em busca de soluções — até a exaustão. A animação abaixo mostra o que você veria em seu computador. No final, restam alguns pontos isolados da região inicial: são os pontos com coordenadas inteiras. Não acredita? As marcas sobre os eixos mostram que as coordenadas são inteiras, e uma contagem direta revela que há exatamente 66 pontos. (Para interromper a animação no último quadro, pressione a tecla Esc (escape). O filme volta a rodar no seu navegador com a tecla F5.) Exercício 2. Além das inequações óbvias (ver acima), que condições adicionais devemos colocar no GrafEq para que o programa selecione exatamente os pontos em ? É necessário traduzir essas condições em equações ou inequações que utilizem as funções disponíveis no GrafEq. Que funções são essas? Obviamente, a técnica aqui ilustrada se aplica a outras regiões. Mostramos abaixo como o GrafEq descobre os 13 pontos em pertencentes ao círculo de raio 2 e centro na origem. 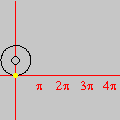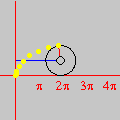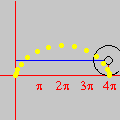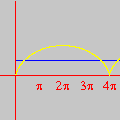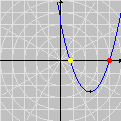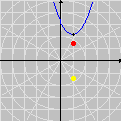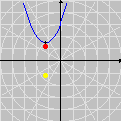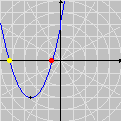(Descubra uma fórmula para este caso.) Em vez de regiões, podemos também considerar curvas no plano; ou seja, podemos usar o GrafEq para resolver equações diofantinas graficamente. Como exemplo, mostramos uma animação que confirma a resposta da Questão 22 (Parte A) do Provão 2002. Um artigo mais detalhado sobre o GrafEq aparecerá na seção Laboratórios. Carlos César de Araújo, 7-8 de agosto de 2002