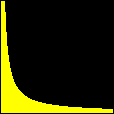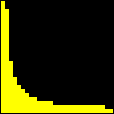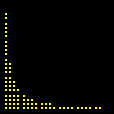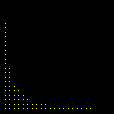
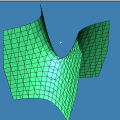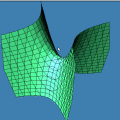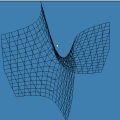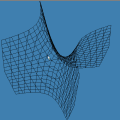
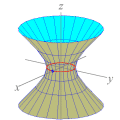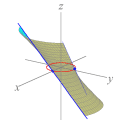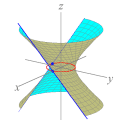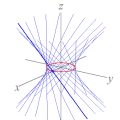
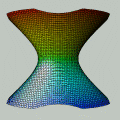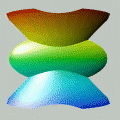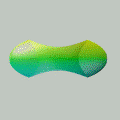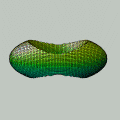
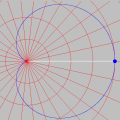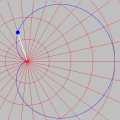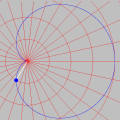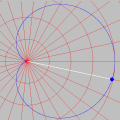
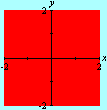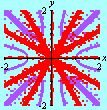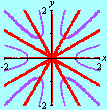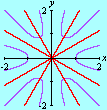
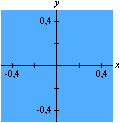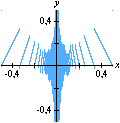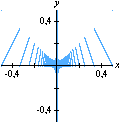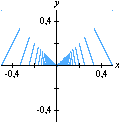
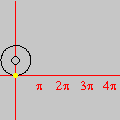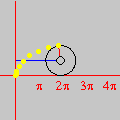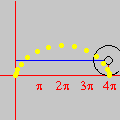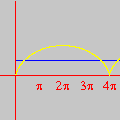
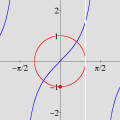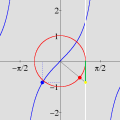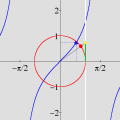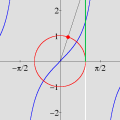
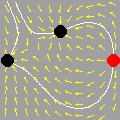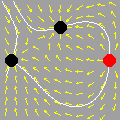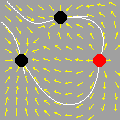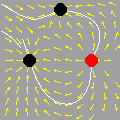
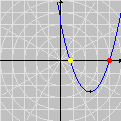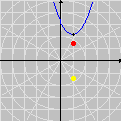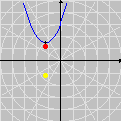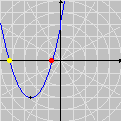
Um Gráfico Interessante Esta animação animação contém 28 aproximações sucessivas do gráfico de sobre o intervalo . Como quisemos ressaltar apenas a curiosa distribuição dos pontos, ocultamos os eixos coordenados. O último quadro contém exatamente 3043 pontos do gráfico! Por "mdc" queremos dizer exatamente o que você está pensando: "máximo divisor comum". A maioria das pessoas fica completamente surpresa diante de tudo isso. Jamais se detiveram sobre a construção de um gráfico como esse. O principal motivo é que estamos habituados a considerar a expressão apenas para valores naturais (pertencentes a ) de a e b. Nesse caso, o que poderia ser ? Faria sentido pelo menos considerar o cálculo de ? Qual seria, afinal, a definição de "máximo divisor comum" utilizada para legitimar tais cálculos? Todas essas questões são discutidas no Capítulo XX do CD Números. Ali é apresentada uma definição de que se aplica a números reais . Mostra-se, também, que o máximo divisor comum de dois números reais nem sempre existe. Em particular, a expressão está definida se e somente se . Portanto, o que você viu são apenas alguns pontos do gráfico da função dada por . Mostramos apenas 3043 pontos de um conjunto infinito de pontos. Tal façanha, evidentemente, só é viável com o auxílio de um computador. De fato, os quadros da animação foram gerados num piscar de olhos por umas poucas linhas de código na linguagem do Mathematica. Entretanto, nem mesmo um computador poderia nos dar o gráfico "completo". Mais ainda, as rotinas gráficas do Mathematica não produzem o gráfico de com a mesma "espontaneidade" de outros gráficos "comuns". É necessário algum conhecimento da Matemática necessária para guiar o programa inteligentemente, ensinando-lhe como selecionar pontos adequados de no intervalo . (Conforme observamos no CD, o GrafEq produz esse gráfico automaticamente.) Aqueles que já estudaram Análise numa universidade provavelmente não serão pegos de surpresa. De fato, a função f  acima é discutida nas páginas 159 e 180 da primeira edição do famoso Curso de Análise de Elon Lages Lima. Entretanto, Lima não menciona explicitamente nenhuma conexão com o cálculo de máximos divisores comuns. É apresentada apenas a seguinte definição: "Seja definida por se é uma fração irredutível com , e ." Acontece que, conforme mostramos no Capítulo XX do CD Números, essa é precisamente a regra que define a partir da definição geral de máximo divisor comum. Algumas propriedades "patológicas" dessa função são demonstradas no livro de Lima. Por exemplo, estenda f  à reta inteira declarando-a nula nos irracionais. O resultado é uma função descontínua em , mas contínua em . Difícil de enxergar? O maior orgulho dos analistas é poder demonstrar as coisas mais óbvias sem qualquer apelo à "intuição"; sem ver nenhum gráfico. Claro, isso é um exagero. Gráficos computadorizados podem ser úteis para sugerir fatos e apontar caminhos quando a intuição falha. Por exemplo, os gráficos da nossa animação nos dão pistas claras sobre eixos de simetria da função f. Tente provar que a reta é um eixo de simetria. Gráficos sobre intervalos maiores revelam uma certa periodicidade. Mostre que f  é periódica e calcule o seu (menor) período.   Carlos César de Araújo, 22 de julho de 2002 NOTA. A partir do Mathematica 7 (lançado quase sete anos após a escrita deste texto), tornou-se possível obter o gráfico de mais facilmente por meio da função DiscretePlot.   Atualizado em 21 de dezembro de 2014