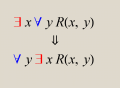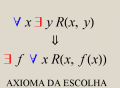Lógica
|

|
It was almost superhuman and a telling indication of
that of which men are capable if their dedication is to creative work and
knowledge instead of cruder efforts to dominate and be known.
Bertrand Russell (ao lado), sobre a obra lógica de Frege. |
A Lógica, particularmente a Lógica
Matemática, despontou no século XX como um dos campos mais fascinantes e
revolucionários do conhecimento humano. Conexões espetaculares com diversas partes da Matemática (Álgebra, Teoria dos Números, Topologia Geral,
Combinatória, Teoria das Categorias), Ciência da Computação, Inteligência Artificial e Robótica se cruzam nas províncias da Teoria da Computabilidade ("Funções Recursivas"),
Teoria dos Modelos e Análise Não-convencional. Nesta seção você verá, sem maiores
delongas filosóficas, por que a Lógica é importante para a Matemática e os fundamentos metodológicos da Ciência em geral.
-
A lógica da Lógica
-
Introdução ao Cálculo Proposicional.
-
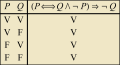
Tautologias
Úteis
-
Lógica e linguagem — Orações adjetivas Quando a Lógica esclarece mais do que a Gramática.
-
Lógica e linguagem — Problemas com a dupla negação. Duas negações nem sempre se cancelam!
-
O Conceito de Conseqüência Lógica.
-
Métodos de Demonstração.
-
Lógica e Matemática — Uma Classificação dos Triângulos. Três espécies de triângulo que podem se reduzir a duas.
-
O Teorema de Hauber.
-
O Cálculo de Predicados.
-
Por Que é Importante Ser Único? Este artigo mostra a relevância de afirmações puras de unicidade.
-
Lógica e Matemática — O Lugar do Vértice. A lógica por trás de um simples problema de Gometria Analítica.
-
Simbolização de proposições matemáticas (Teoria dos Números).
-
Simbolização de proposições matemáticas (Análise e Topologia)
-
Lógica e Matemática — O Óbvio que Induz o Não Óbvio. Um exemplo de como transformações lógicas simples podem revelar algo inteiramente novo a partir de um fato trivial.
-
O significado da Indução Matemática.
-
Lógica e Matemática — Uma Aplicação da Indução. Um resultado a meio caminho entre a indução clássica e a indução estrutural.
-
Indução Estrutural.
-
Uma Demonstração do Teorema de Cantor. Veja como um pouco de lógica simbólica permite descobrir e provar um dos resultados mais célebres da Matemática.
-
Usos do Método Diagonal de Cantor
-
O Paradoxo de Cantor. Conforme escreveu Paul Halmos certa vez, "Nada contém tudo".
-
O Paradoxo de Russell.
-
O Paradoxo de Richard.
-
Os
Axiomas de Zermelo-Fraenkel
-
O
Axioma da Escolha
-
Funções
de Skolem
-
Introdução
à Teoria dos Modelos (linguagens e estruturas)
-
Categoricidade e a Conjectura de Carnap.
-
O
Teorema de Löwenheim-Skolem
-
A Lógica em Concursos no Brasil
Artigos Relacionados (Outras Seções)
Citamos abaixo outras páginas do site que (no momento) lidam com tópicos de Lógica.
-
Lógica e Linguística Um curso prático de 32 horas.
-
O Problema 11 da seção Provas e Problemas Resolvidos.
-
Artigos da seção Conceitos Fundamentais.
-
Artigos da seção História.
-
Artigos da seção Erros.
GeT no Facebook
A partir de janeiro de 2014 comecei a publicar sobre Lógica e Matemática no nosso perfil no Facebook.
Publicações Relevantes
Uma parte significativa dos melhores periódicos devotados à Lógica
se acha escrita em inglês. Os exemplos colhidos abaixo são especialmente interessantes não só pela EXCELENTE qualidade dos artigos,
mas principalmente por apresentarem textos on-line, gratuitamente. Um verdadeiro banquete intelectual! Alguns dos artigos dessas publicações
serão comentados numa seção especial deste site.
Carlos César de Araújo, 28 de fevereiro de 2014


 LEMUS
LEMUS