Lógica e Matemática
Uma Aplicação da Indução
Carlos César de Araújo

Introdução

Como se sabe, o Princípio da Indução Matemática (em sua versão clássica) fornece um método para provar sentenças do tipo

(1)

onde é uma propriedade aplicável a números naturais e . Em sua forma fraca, mais simples, a técnica repousa sobre o fato de (1) ser logicamente equivalente a

(2)

(A equivalência entre (1) e (2) pode ser proposta como uma definição, aceita como um axioma ou derivada como um teorema. Veja o artigo Indução desta seção.)

Também é amplamente sabido que o método acima se aplica a objetos diferentes dos números naturais, contanto que possuam alguma característica mensurável por esses números. Então, pode-se tentar provas indutivas em usando essa “medida”. Exemplificando, a fim de provarmos que todo polígono satisfaz uma certa propriedade, podemos fazê-lo por “indução no número de lados” da seguinte maneira: (i) verificamos a propriedade para polígonos de três lados; (ii) mostramos que se a propriedade valer para polígonos de lados, continuará válida para polígonos de lados.

O exemplo dos polígonos nos permite conceber facilmente o caso geral: dada uma função , trata-se de provar afirmações da forma

por “indução em ”. Isto é menos óbvio quando não ocorre em . (Um exemplo em que ocorre em é: “[Num domínio de integridade] todo polinômio de grau [] possui no máximo zeros.”)

Surpreendentemente, não é fácil encontrar um enunciado geral desse método nos compêndios. Por exemplo, não encontramos uma formalização em textos como [2] e [4], escritos por lógicos eminentes num período em que [1] ditava os padrões de rigor na Matemática. Uma exceção recente é [3] (Cap. 1, p.39), mas o autor deixa a demonstração como exercício, numa forma não imediatamente reconhecível. Seja como for, neste artigo preenchemos essas lacunas registrando o procedimento e, principalmente, justificando-o de maneira simples e direta.

Enunciado do Procedimento

A técnica de indução à qual nos referimos envolve os seguintes componentes:

• um conjunto ;

• uma função .

• um tal que .

Por exemplo, se é o conjunto dos polígonos, então pode ser o número de lados. Nesse caso, , já que todo polígono tem no mínimo três lados.

Voltando ao caso geral, suponha que se queira provar

(3)

“por indução” em . O plano consiste em dois passos:

Passo 1. Prove que se um qualquer é tal que , então ;

Passo 2. Tome um “arbitrário” e admita a seguinte hipótese de indução: se um é tal que , então . Deduza que se um é tal que , então .

Antes de mostrarmos como (3) é conseqüência desses passos, lembramos que o sucesso dessa estratégia não pode ser garantido de maneira absoluta, pois depende da propriedade e de uma escolha acertada da função . O Passo 2 envolve a transição mais difícil: nos casos em que é possível passar de para , a função sempre reflete alguma característica estrutural dos elementos de que pode ser especificada recursivamente a partir de uma definição indutiva de . Isso conduz naturalmente ao exame da indução estrutural, assunto de outro artigo desta seção.

Demonstração

Vejamos como os passos (1) e (2) implicam (3). Cremos que a conexão ficará mais transparente se usarmos livremente a linguagem dos conjuntos. Em particular, usaremos a notação para a imagem inversa de por . Um momento de reflexão mostra que a afirmação a ser provada no Passo 1 é

(4)

onde, por comodidade, cometemos o abuso de empregar a mesma letra () para denotar uma propriedade e o conjunto correspondente. Fica claro, então, que o Passo 2 consiste em provar

(5)

(É intuitivamente óbvio que o Passo 2 equivale à derivação desta sentença, mas isto pode ser rigorosamente estabelecido por meio do Teorema da Dedução do Cálculo de Predicados.)

Justificaremos o procedimento se mostrarmos que (4) e (5) acarretam (3) na forma

Suponha que (4) e (5) foram provados. Então temos um caso de (2), com . Segue-se do Princípio da Indução que

Mas esta sentença é equivalente a

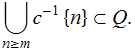(6)

(Veja o artigo A União é o Supremo.) Ora, por hipótese, , condição que é equivalente a

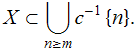(7)

Resulta  de (6) e (7) que . Era o que devíamos provar.

Em suma, podemos dizer que uma prova de (3) por “indução em ” corresponde a provar por “indução em ”.

Exercícios

Exercício 1. Outra maneira de provar (3) por indução é a seguinte. Dado , suponha que do fato de valer para todo tal que , se possa concluir que vale para todo tal que . Justifique este procedimento usando o Segundo Princípio da Indução.

Exercício 2. Em nossa apresentação, há alguma restrição sobre que permita concluir algo sobre sua cardinalidade? Por exemplo, podemos concluir que , isto é, que deve ser no máximo um conjunto infinito enumerável?

Referências

[1] Bourbaki, Nicholas. Elements of mathematics I, Theory of sets. Hermann, 1968.

[2] Feferman, Solomon. The Number Systems: Foundations of Algebra and Analysis. Reading, Mass.: Addison-Wesley Publishing Co., Inc., 1964.

[3] Mitchell, John C. Foundations for Programming Languages, MIT Press, 1996. (O capítulo 1 se encontra disponível em http://theory.stanford.edu/~jcm/books.html.)

[4] Rosser, J. Barkley. Logic for mathematicians, McGraw-Hill, New York, 1953.

Carlos César de Araújo, 20 de janeiro de 2007, 18:52:44