Lógica e Matemática
O Lugar do Vértice
Carlos César de Araújo

Introdução

Em vários cursos que ministrei com o Winplot, percebi que um dos exercícios mais instigantes é a descoberta da trajetória descrita pelo vértice da parábola durante a variação do coeficiente (enquanto os demais são mantidos fixos). O problema surge naturalmente porque, em geral, os estudantes conhecem as influências de e sobre o gráfico, mas nada sabem sobre o significado geométrico de . É como um subproduto desse estudo com o software — e não como um divertimento acidental — que se percebe (ou se pode fazer perceber) o aparente movimento do vértice sobre uma parábola de concavidade oposta.

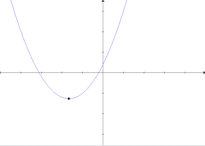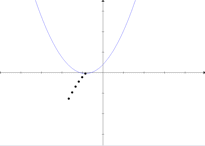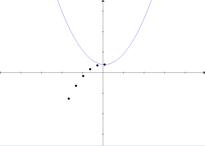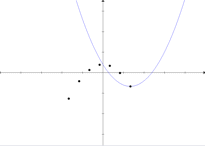
Surge a questão: como ter certeza de que a trajetória do vértice é mesmo uma parábola? Na Matemática, o instrumento da certeza (embora nem sempre o da descoberta) é o raciocíno lógico dedutivo. A lógica por trás desse problema nos conduzirá a algumas idéias interessantes. Mas vejamos, primeiro, uma dedução “informal”, isto é, sem Lógica (o que não quer dizer que seja ilógica).

Solução sem Lógica

Nosso problema não ofereceria dificuldade alguma para um matemático, digamos, do século XVIII. Exceto por  detalhes de notação e exposição, ele poderia argumentar como segue. Dado , o vértice da parábola é o ponto

Vértice da parábola

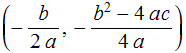
de modo que o lugar geométrico do vértice quando varia é descrito pela equação que se obtém do sistema

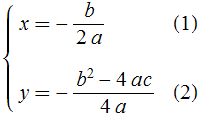
por eliminação da variável . A eliminação é fácil: basta tirar o valor de na primeira equação,

e substituí-lo na segunda, o que nos dá

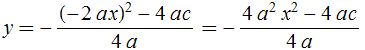
ou

Equação cartesiana do lugar

Essa equação quadrática em confirma que o lugar do vértice é mesmo uma parábola com concavidade oposta à da original. No século XXI, temos a sorte de poder visualizar rapidamente a justeza do resultado num software simples como o Winplot.

Dificuldades

A solução anterior é sucinta e direta. É típica do padrão de apresentação que se vê em muitos textos de Matemática: parte-se de algumas fórmulas, montam-se algumas equações, manipulam-se algumas variáveis e destaca-se uma equação final. Mas está longe de satisfazer aos espíritos mais inquiridores, inexperientes e que padecem com o mal ensino dessa ciência. Por que a eliminação conduz à resposta? O que significa exatamente “eliminar” uma variável? O que está “variando”? Qual a relação entre a variação de , que gera a trajetória, e a equação final?

Essas indagações remetem a noções e processos lógicos que o solucionador treinado articula apenas em sua mente, talvez de forma nebulosa; mas tendo “assimilado-os” durante anos de estudo, prática e “confirmação”, já não vê motivo para explicitá-los numa apresentação comum. (É o postulado tácito do isomorfismo da compreensão.) Uma vez revelados, contudo, tais processos estabelecem conexões inesperadas entre os mais variados temas.

Retomada: primeiro, uma bi-implicação

A trajetória do vértice é um conjunto de pontos do plano cartesiano (), que chamaremos de (para realçar a dependência dos coeficientes mantidos “fixos”). A maneira lógica de identificar um conjunto é através de uma propriedade que o caracteriza — no caso, uma condição que um ponto deve satisfazer para pertencer a . Como é de se esperar neste contexto, por “condição” entende-se uma equação cartesiana, digamos, (ou apenas , se se quiser deixar implícitos como “parâmetros” na discussão), tal que tenhamos, para todo ,

Bi-implicação (1)

A idéia é identificar a partir da forma da equação. A falta de clareza total e absoluta com relação a essa bi-implicação  — um fato elementar, mas crucial —  é conseqüência do ensino da Geometria Analítica sem a devida atenção à Lógica. Não admira que muitos estudantes “aprendem” essa matéria sem nunca terem compreendido o que realmente estiveram fazendo com curvas e equações.

A Condição do Lugar

O conjunto é obtido variando-se no vértice da parábola. Isto significa: na expressão do vértice, atribua a todos os valores reais e reúna os resultados num conjunto. Conseqüentemente,

A trajetória como um conjunto de pontos

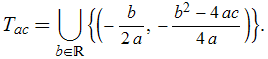
Essa igualdade encerra um quantificador existencial: significa que, para todo , tem-se

Bi-implicação (2)

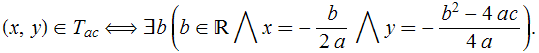
Comparando isso com a bi-implicação anterior, resulta que

Bi-implicação (3)

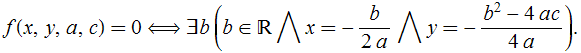
Observemos atentamente essa expressão. No lado esquerdo queremos apenas uma equação relacionando quatro  “grandezas” ( e ). Mas, no lado direito, temos duas equações e uma variável a mais (). Não há nenhuma contradição aqui, pois a variável aparece ligada a um quantificador. Na terminologia de Peano (hoje em desuso, embora muito pertinente), a ocorrência de no lado direito não é “real”, mas aparente; nada é dito sobre . Assim, os dois lados efetivamente contêm as mesmas variáveis livres (ou, se quisermos, as mesmas variáveis sob o efeito de quantificadores universais).

Eliminar o quê?

Vemos agora que, para acoplar as equações em e , devemos eliminar o quantificador . É isto: eliminar significa, na realidade, eliminar o quantificador existencial . Mais precisamente, significa banir (e o que estiver sob o seu efeito) a troco de uma condição logicamente equivalente nas demais variáveis ( e ). De acordo com a nossa solução informal, essa condição é Portanto, sejam quais forem , com , é verdade que

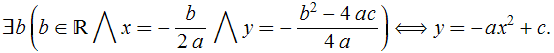
Não obstante, a solução informal prova apenas a parte . A rigor, a recíproca não foi provada. Mas este é um caso muito especial (devido ao grau de na primeira equação) em que a prova da recíproca é fácil (embora, talvez, algo impalpável para o principiante), de modo que podemos deixá-la aos cuidados do leitor.

Eliminação de Quantificadores

Alternativamente, pode-se obter a equação do lugar num só passo como uma aplicação da equivalência lógica (examinada em outro artigo desta Seção)

Este é o caso mais simples do que se conhece em Lógica como eliminação de quantificadores: uma sentença com quantificadores é transformada numa equivalente, mas sem rastro de quantificação. Problemas de “eliminação de variáveis” como o que vimos — além de outros já apresentados neste site — são, quando vistos mais de perto, problemas de eliminação de quantificadores, e surgem em muitas partes da Matemática “pura” e “aplicada”, mesmo nas mais elementares.

Podemos citar mais um exemplo sem abandonar o trinômio quadrático. Sabe-se que o trinômio   () possui raízes reais se, e somente se, . Em termos mais explícitos, isso significa que, dados , vale

Note-se que temos um quantificador no lado esquerdo da bi-implicação, mas nenhum no lado direito — foi eliminado!

Existe uma maneira sistemática — um algoritmo — para eliminar quantificadores? Seria formidável dispor de um tal procedimento, já que poderíamos delegar o trabalho a uma máquina, permitindo-nos concentrar apenas na modelagem ou especificação dos problemas em linguagem lógica. Por volta de 1930, motivado por um problema na interseção da Geometria com a Lógica, o lógico polonês Alfred Tarski anunciou o primeiro algoritmo para a eliminação de quantificadores atuando sobre equações e inequações polinomiais com coeficientes reais. Apesar de sua importância, o método de Tarski não é prático. Uma implementação mais eficiente só surgiria quase quarenta anos depois. Atualmente, várias técnicas de eliminação têm sido investigadas por pesquisadores de várias áreas, muitos dos quais movidos pela beleza intrínseca do assunto. Mais recentemente (2000), Adam Strzebonski desenvolveu um método que foi incorporado nas funções Resolve e Reduce do software Mathematica 5. (A função Eliminate, existente desde a versão 1, é suficiente para o nosso problema, mas lida apenas com equações à maneira do nosso matemático do século XVIII — que nada sabe de quantificadores.)

A eliminação de quantificadores também é assunto da seção Álgebra (!) deste site.

Exercício

Visualização (por si só) não implica compreensão. (Pelo menos, nem sempre!). Verifique que já era possível visualizar o lugar do vértice no Winplot a partir das equações iniciais sem recorrer à eliminação de variáveis. (Use a janela de equações paramétricas do Winplot. A trajetória parametrizada foi vista aqui.) Como se poderia explicar a forma da trajetória sem a eliminação?

Carlos César de Araújo, 23 de dezembro de 2006, 18:44:34