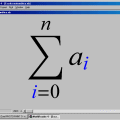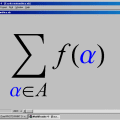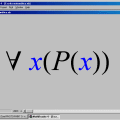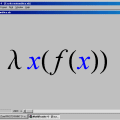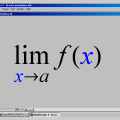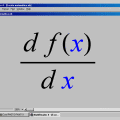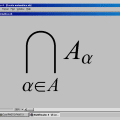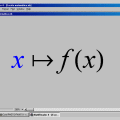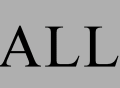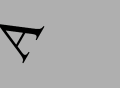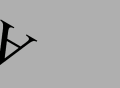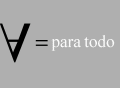Escrita Matemática In a very real sense, the writer writes in order to teach himself, to understand himlself; the publishing of his ideas, though it brings gratifications, is a curious anticlimax. Alfred Kazin (1915-1998) Se alguém vir um erro de português neste site, ou mesmo uma construção que ofenda práticas estilísticas abonadas, não tenha dúvidas: registre tudo por escrito e remeta ao autor. Os matemáticos também sabem escrever! Pensa-se vulgarmente que o envolvimento com números destrói a região do cérebro responsável pelo bom uso da linguagem. Falso! Lord Bertrand Russell foi um lógico que conheceu os pináculos da abstração matemática. No entanto, soube escrever suficientemente bem para merecer o Prêmio Nobel de Literatura em 1950 (pela obra Ensaios Céticos). Russell foi apenas uma estrela de uma enorme constelação de mestres da exposição matemática. Outras figuras de relevo que guardo comigo são o brasileiro Elon Lages Lima, o húngaro Paul Halmos e o norte-americano Donald Knuth. As primeiras obras cujos autores me impressionaram pela clareza e fluência do estilo foram Matemática Clássica, de P. J. Hilton e H. B. Griffiths (edição brasileira de 1975, em três volumes), e Introdução à Análise Linear, de D. Kreider, R. Kuller, D. Ostberg e F. Perkins (também publicada no Brasil em três volumes). Aprendi a escrever Matemática observando meticulosamente as frases desses expositores: a maneira como iniciavam certos períodos, a colocação dos indicadores de inferência, as ocasionais tiradas humorísticas, as vírgulas, o emprego de expressões do Latim, as analogias engenhosas, os parágrafos de motivação — enfim, tudo o que é relevante para a beleza arquitetural de um texto científico. Todos aqueles que escrevem Matemática com freqüência acabam seguindo certas normas (muitas vezes inconscientemente). Por exemplo, algumas pessoas quebram uma cadeia de igualdades em linhas que terminam com esses sinais, ao passo que outras preferem uma coluna de igualdades mais ou menos no centro, alinhando o todo. Questões desse tipo passaram a receber tratamento sistemático com o advento de sistemas de composição como o TeX e o LaTeX, os quais colocaram nas mãos dos autores as preocupações que eram parte do ofício dos tipógrafos. Mas é interessante notar que, muito antes disso, vários matemáticos sugeriram diretrizes estilísticas e notacionais. Lógicos distantes como Leibniz e Alfred Tarski se preocuparam em elaborar sistemas de notações adequados para a expressão das idéias matemáticas. Portanto, um bom texto de Matemática exige muito mais do que o domínio da Gramática. Além da escrita de palavras, deve-se atentar também para a escolha adequada dos símbolos, a boa disposição das equações, a colocação dos diagramas, etc. Em se tratando de publicações "eletrônicas", como as deste site, novos elementos entram em cena (links, botões, animações). Por surpreendente que pareça, aqui também vigoram normas estilísticas, e as discussões decorrentes de qualquer apreciação estética. Qual a ordenação mais agradável dos termos de uma equação longa? Escolheremos colchetes ou parênteses para delimitar matrizes? Denotaremos as constantes lógicas por símbolos ou por palavras? Há um limite aceitável para o emprego de notações lógicas? Esses são alguns dos temas que pretendemos discutir nos artigos desta seção. Muitos deles caberiam num curso tradicional de "Metodologia Científica" (se a ABNT tivesse respostas para todos). Outros cairão na interseção de áreas como a Lógica e a Lingüística. Minhas principais fontes de inspiração para esta parte foram os seguintes textos (ultrapassados em certos pontos, mas ainda interessantes): E. J. McShane, Mantaining communication, Amer. Math. Monthly, 1957, pp. 309-317. J. L. Doob, L. Carlitz, F. A. Fricken, G. Paranja and N. E. Steenrod, Manual for authors of mathematical papers, Bull. Amer. Math. Soc. 68 (1962), pp. 429-444. Four Panel Talks on Publishing - I. Why publish (L. Gillman), II. What to publish (Paul Halmos), III. Publication related to teaching (H. Flanders), IV. How to publish (Beatrice Shube), Amer. Math. Monthly, 1975, pp. 13-21. Donald Knuth, Mathematical Typograpy, Bulletin of the American Mathematical Society, 1979, pp. 337-372. R. P. Boas, Can we make mathematics intelligible?, Amer. Math. Monthly, 1981, pp. 727-731. Descobri esses e outros encantadores artigos enquanto vasculhava volumes de periódicos nas bibliotecas da UFMG, há vários anos. Hoje, basta digitar "mathematical writing" num campo de busca para se deparar com uma enxurrada de textos isomorfos do gênero. Em particular, recomendo especialmente a leitura do seguinte livro (disponível eletronicamente no formato dvi): Knuth, Donald E, T. Larrabee and P.M. Roberts, Mathematical Writing, MAA Notes Series 14, Math Association of America, 1989. Mais recentemente, os criadores do Mathematica têm discutido várias questões que, segundo penso, influenciarão o futuro da escrita matemática. O link abaixo aponta para o texto de uma palestra proferida por Stephen Wolfram. Mathematical Notation: Past and Future. Em janeiro de 2003 tive a satisfação de descobrir um delicioso livreto, o The Handbook of Mathematical Discourse, de Charles Wells. Fiquei surpreso com a semelhança entre os objetivos desse autor e os meus, dado que há anos venho colecionando observações lingüísticas com o mesmo propósito (muitas das quais coloquei no site de Jeff Miller (Earliest Known Uses of Some of the Words of Mathematics). Artigos do site Matemática por e-mail. Ambigüidades Notacionais. O tal do tal que. Nomes para os coeficientes de um polinômio. Usos do alfabeto grego. Convenções na Geometria. Solecismos matemáticos. Nomeando espaços topológicos. Funções anônimas. Como traduzir um termo técnico? Escrevendo artigos com o LaTEX. Preparando-se para a MathML Programação de Notações com o Mathematica. SOFTWARES Conheça este formidável pacote de programas para a produção de documentos científicos baseados no TEX. (Para plataforma Windows.) Carlos César de Araújo, 19 de julho de 2003