Lógica e Matemática
O Óbvio que Induz o Não Óbvio
Carlos César de Araújo

Introdução

Neste artigo enunciaremos um resultado sobre o conjunto dos números naturais que pode ser considerado bastante “óbvio”, mas (relativamente) pouco conhecido. Em seguida, passaremos o enunciado para a linguagem simbólica da Lógica e faremos algumas manipulações simples com quantificadores e conectivos (discutidas em outros artigos desta Seção), gradualmente transformando o enunciado original num outro equivalente. A surpresa é que, no final, obtemos um fato totalmente “diferente” que, embora mais familiar, é normalmente considerado muito menos óbvio.

Um Fato Óbvio

Um conjunto de números naturais pode não possui um maior elemento, mas tem sempre um menor, um primeiro. Não há como duvidar disso. É um fato que se pode aceitar como óbvio. Não importa se preferimos começar com ou : qualquer deve “começar” em algum número, que é o seu elemento mínimo — o menor de todos.

Observe que ao falarmos em “qualquer ”, incluímos o caso . Afinal, . Todavia, o conjunto vazio é a única exceção à regra — o que também não deixa de ser óbvio, uma vez que não possui elemento algum (donde muito menos um menor). Assim, devemos consertar nossa afirmação e dizer: se e , então possui um menor elemento.

Tradução para a o Simbolismo Lógico

Uma formulação mais completa deve mencionar o quantificador “qualquer” que atua sobre , o que pode ser feito assim:

Expressão (1)

Por exportação, isto é o mesmo que

Expressão (2)

Agora, a sentença “ possui um menor elemento” se decompõe na seguinte:

Expressão (3)

(veja o artigo Teoria da Ordem na seção Conceitos Fundamentais), que por sua vez é equivalente a

Expressão (4)

obtida da anterior por contraposição da implicação.  Substituindo a expressão (4) na expressão (2), ficamos com a seguinte asserção:

Expressão (5)

Tomando a contrapositiva da segunda implicação dessa sentença, o enunciado (1) torna-se

Expressão (6)

Dualidade Booleana

As fórmulas “” e “” na sentença (6) nos levam a considerar o seu dual booleano. Conforme vimos em outro artigo desta Seção, uma instância da dualidade booleana — que é de largo emprego — provém do fato de toda afirmação da forma (aqui particularizada a )

ser equivalente a

obtida da primeira substituindo (cada ocorrência de) por , que é o complementar de em relação a . Por simplicidade, escrevamos

Desse modo, o dual booleano da sentença (6) é

que é o mesmo que

Expressão (7)

O Passo Final

Por fim, eliminamos o sinal aplicando as regras de negação e a forma normal disjuntiva da implicação:

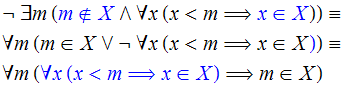
Levando a última expressão na sentença (7), ficamos com o seguinte:

Expressão (8)

Um Fato Popular

Todas as manipulações que fizemos acima, da sentença (1) à sentença (8), alteram a estrutura sintática das sentenças, mas não sua semântica. Por outras palavras — embora não pareça —, a sentença (8) traduz exatamente o mesmo estado de coisas que o fato óbvio com o qual começamos. Agora, paremos para examinar nossa sentença final. Ela nos diz o seguinte:

(1) Considere um conjunto de números naturais (ou seja, );
(2) Tome um número qualquer. (Isso prepara o terreno para o que virá no escopo do quantificador .);
(3) Suponha que do fato de todo predecessor estrito de pertencer a (isto é, ), se possa concluir que também pertence a ().
(4) Então pode-se concluir que todo elemento de pertence a (ou seja, ).

Em vez de conjuntos (de números naturais), podemos falar em propriedades. Nesses termos, a expressão (8) incorpora um método para demonstrar afirmações da forma , onde é uma propriedade sobre números naturais (isto é, ). Logo, a fim de provarmos que é verdadeira para todo , seguimos os mesmos passos acima, começando com (2). Ou seja, assumimos como hipótese que e daí tentamos provar que vale . Se tivermos sucesso em fazê-lo, sem nenhuma restrição sobre , então teremos conseguido provar que é sempre verdadeira em .

Esse método de prova é popularmente conhecido como Princípio da Indução Forte ou Segundo Princípio da Indução, para diferenciá-lo da indução matemática em sua forma mais corriqueira (a do “raciocínio de para ”). A relação de “força” entre essa duas formas de indução finita é tema de outro artigo desta Seção.

Óbvio, mas não Anônimo

Tendo mantido o suspense até este ponto, podemos revelar agora que o fato óbvio do qual partimos também tem um nome na literatura: Princípio da Boa Ordenação. Na teoria da ordem, dizemos que o “conjunto” é bem ordenado. (Veja o artigo Teoria da Ordem, Parte 3 na Seção Conceitos Fundamentais.) Assim, o que mostramos em nossa transição da sentença (1) para a sentença (8) é que a condição de boa ordenação é equivalente a uma forma forte de indução.

Uma Prova Tortuosa

Nos textos “ortodoxos” de matemática, essa equivalência não é explicitamente declarada; a maioria dos autores deriva apenas uma parte da dupla implicação, a saber, que o Segundo Princípio da Indução decorre do Princípio da Boa Ordenação (reforçando nossa opinião de que o primeiro é tomado como menos óbvio) — e isso de maneira indireta, por redução ao absurdo. Resumidamente, o argumento é o seguinte. Assuma que é bem ordenado. Agora, tome e suponha (hipótese de indução) que . Devemos provar que . Por absurdo (sic), admita que , isto é, que . Então possui um mínimo, digamos, . Logo, . Mas isso, com a hipótese de indução, nos dá . Aqui surge a contradição: .

Esse argumento é logicamente impecável, mas é tortuoso. Nossa argumentação, por outro lado, expõe a essência lógica dos enunciados de uma maneira “limpa” e direta, mostrando que o Segundo Princípio da Indução é essencialmente a seguinte variação (do dual booleano) da sentença (2):

Expressão (9)

Além disso, talvez torne mais evidente que os passos se aplicam a qualquer conjunto munido com uma relação que se comporte como a relação menor ou igual a em . (Isso inclui partes do próprio !) Essa generalização é um fato tão poderoso quanto espantoso, sobre o qual falaremos em outra ocasião.

Carlos César de Araújo, 11 de dezembro de 2006, 23:16:07