e 
denotam conjuntos:
Lógica e linguagem
Orações adjetivas
Carlos César de Araújo
Matemática para Gregos & Troianos
A Lógica é uma disciplina útil não só para os fundamentos da Matemática, mas também para um entendimento mais organizado dos mecanismos da nossa própria linguagem. Nesta página veremos um exemplo de como certas distinções gramaticais consideradas difíceis se tornam mais simples quando analisadas com o auxílio de noções lógico-matemáticas elementares.
Observem atentamente as duas frases abaixo, nas quais e denotam conjuntos:
(1) Os elementos de 
que pertencem a 
pertencem a 
.
(2) Os elementos de 
, que pertencem a 
, pertencem a 
.
Várias sentenças estudadas nas gramáticas tradicionais têm uma dessas formas. Eis dois exemplos concretos:
(1) Os homens que são sábios estão cheios de dúvidas.
(2) Os homens, que são sábios, estão cheios de dúvidas.
Voltando à forma geral, podemos dizer que, sintaticamente, obtemos (2) de (1) pela simples inclusão de duas vírgulas:
(1) Os elementos de 
que pertencem a 
pertencem a 
.
(2) Os elementos de 
que pertencem a 
pertencem a 
.
Também podemos perceber, sem demora, que há uma diferença de significado na passagem de (1) para (2). A dificuldade começa quando tentamos exprimir essa diferença com clareza.
O ponto de vista do gramático
Um gramático começaria dizendo que em (1) temos uma oração subordinada adjetiva restritiva
ao passo que em (2) temos uma oração subordinada adjetiva explicativa.
Convém recordarmos rapidamente as definições de alguns desses termos gramaticais. Em (1) e (2) temos orações por causa da presença de um verbo (pertencer). As orações acima destacadas são:
• subordinadas porque dependem de uma outra oração principal;
• adjetivas porque exercem o papel semelhante ao de um adjetivo (de um termo da oração principal). Essas orações são freqüentemente introduzidas por pronomes relativos tais como que, quem, cujo, o qual, etc.
A oração adjetiva restritiva é assim chamada porque efetivamente restringe o significado da principal. Isto não ocorre com a oração adjetiva explicativa, que simplesmente acrescenta uma explicação (sic).
Uma diferença fundamental entre esses dois tipos de orações adjetivas é a seguinte:
• uma oração adjetiva restritiva nunca se apresenta separada por vírgulas — sendo lida sem pausa;
• uma oração adjetiva explicativa sempre se apresenta separada por vírgulas.
Eis uma segunda diferença, comumente citada nas gramáticas:
• uma oração adjetiva restritiva não pode ser omitida sem prejuízo para a compreensão do período;
• uma oração adjetiva explicativa pode ser omitida sem prejuízo para a compreensão do período.
É instrutivo examinar o nosso tema em outra línguas, particularmente o inglês, onde os equivalentes de (1) e (2) seriam escritos como segue:
(1) The elements of 
that belong to 
belong to 
.
(2) The elements of 
, which belong to 
, belong to 
.
Aqui, o efeito da virgulação é o mesmo que em português. Mas é interessante notar a diferença (polêmica) no emprego dos pronomes relativos:
• that é usado em orações adjetivas restritivas.
• which é usado (ou fortemente recomendado) em orações adjetivas explicativas.
(No Mathematical Writing de Donald Knuth — citado na seção Escrita Matemática deste site — há uma interessante discussão sobre Which vs that por Mary-Claire.)
Explicação pela Lógica
Para os que estudam Lógica, a diferença entre os significados de (1) e (2) pode ser expressa de maneira bem simples em termos de operações e relações entre conjuntos. Vejam:
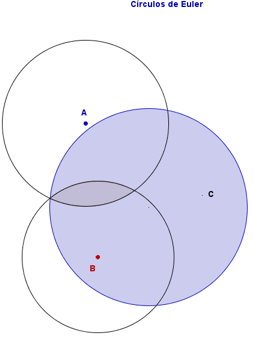
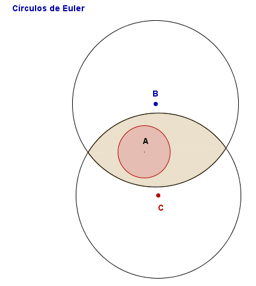
Essas simples formulações contêm tudo o que necessitamos para uma análise dos significados de (1) e (2). Por exemplo, retomemos a concessão do gramático, de que a proposição expressa pela adjetiva explicativa (
) em (2) pode ser “omitida sem prejuízo para a compreensão do período”. É óbvio que, em se tratando de proposições — orações declarativas — essa omissão nem sempre é correta: afirmar “
e 
” não é o mesmo que afirmar “
”. Contudo, isto seria possível uma vez fixado um contexto no qual 
fosse pressuposta (como no caso de um axioma). Nesse caso, tudo se passa como se a intenção fosse afirmar que 
, a menção de “
” servindo apenas para recordar um fato conhecido ou aceito.
Podemos tornar ainda mais clara a diferença entre (1) e (2) notando que uma proposição do tipo
é logicamente equivalente a
Isto é facilmente compreendido por meio de círculos de Euler (que não são a mesma coisa que os diagramas de Venn), embora possa ser provado com base na tautologia
(Veja Lista de Tautologias Úteis, nesta seção.)
Em resumo, temos:
Em (1) temos a afirmação de que os elementos comuns a 
e 
estão em 
. Em (2) temos a afirmação de que os elementos de 
estão entre os elementos comuns a 
e 
.
Podemos dar um passo a mais e dizer que (2) é mais forte que (1), no sentido de que (2) implica (1). Pois se
então, pelo fato de a interseção preservar inclusões,
Deste modo, se 
, então 
.
Curiosamente, do ponto de vista da força lógica, a frase que contém a oração adjetiva explicativa é mais restrita do que a que contém a oração adjetiva restritiva!
25 de fevereiro de 2006, 15:36:41