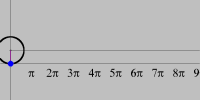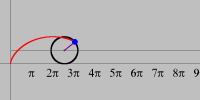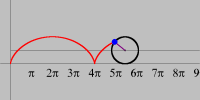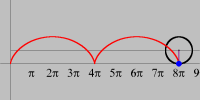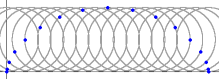
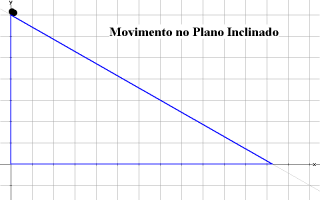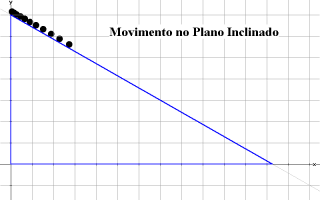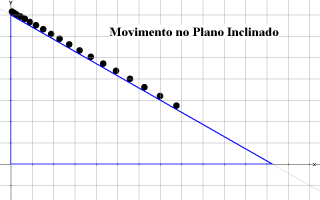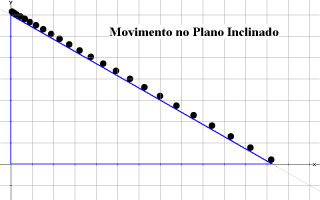
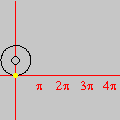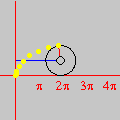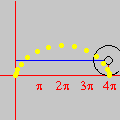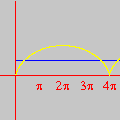
A Ciclóide no Winplot Os quadros desta pequena animação foram produzidos no Winplot e depois reunidos num único arquivo para uma exibição equivalente a 10 cenas por segundo. A montagem final foi feita no Mathematica. Contudo, é fácil produzir e apreciar o mesmo movimento no próprio Winplot. O filme mostra a trajetória descrita por um ponto da periferia de uma roda que se desloca em linha reta com velocidade constante (relativamente a um observador em repouso). A curva traçada é chamada ciclóide e resulta da composição de dois movimentos: um circular e outro retilíneo. A figura abaixo, semelhante a uma fotografia estroboscópica do movimento, também foi produzida no Winplot. Para traçar uma ciclóide no Winplot, é necessário fornecer ao programa as equações dessa curva. Essas equações não são (normalmente apresentadas como sendo) do tipo cartesiano comum, e sim paramétricas: descrevem a curva como um conjunto de pares ordenados cujas componentes são funções de um parâmetro — uma variável que percorre um certo intervalo. Com base nas equações, pode-se obter tanto o gráfico estático da ciclóide como uma animação que mostra o traçado da curva gradualmente. Caso você queira entender os conceitos matemáticos e as técnicas utilizados na produção de animações como essa no Winplot, visite a seção Laboratórios de Matemática e estude o artigo Introdução ao ambiente 2D do Winplot. A partir daí, você estará em condição de reproduzir várias outras experiências cinemáticas conhecidas (movimento num plano inclinado, lançamento de projéteis, etc.). A criação de tais simulações no Winplot constitui um exercício extremamente instrutivo, não apenas pela excelente combinação de conhecimentos de Matemática (Geometria Analítica e Cálculo Vetorial) e Física, mas também por exigir criatividade para contornar possíveis limitações do software. Nada comparável se encontra nos fastidiosos testes tradicionais. Além disso, o estudo do Winplot facilita o contato com softwares mais sofisticados que exigem amplos conhecimentos de programação, como é o caso do Mathematica. Assim que você conseguir domesticar essas pequenas inteligências artificiais, a sua relação com a Matemática nunca mais será a mesma! Carlos César de Araújo, 14 de agosto de 2002