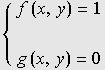Uma visão diferente das raízes da unidade Para cada número natural , as raízes n-ésimas da unidade são os números complexos z que satisfazem a equação . Reunindo as soluções complexas de todas essas equações, obtém-se o conjunto das raízes da unidade  — o qual inclui as raízes quadradas, cúbicas, quartas, etc. A visão geométrica mais comum das raízes da unidade é como vértices de certos polígonos no plano complexo. Mais precisamente, as raízes n-ésimas constituem os vértices de um polígono regular de n lados inscrito na circunferência unitária. Por exemplo, as raízes cúbicas () dividem a circunferência unitária em três partes iguais. 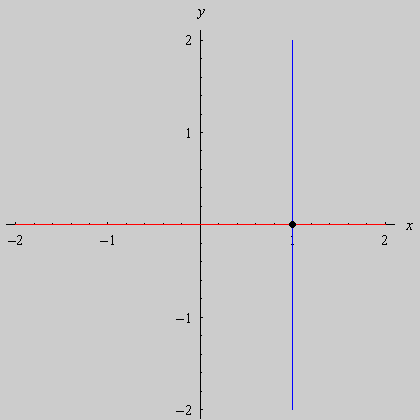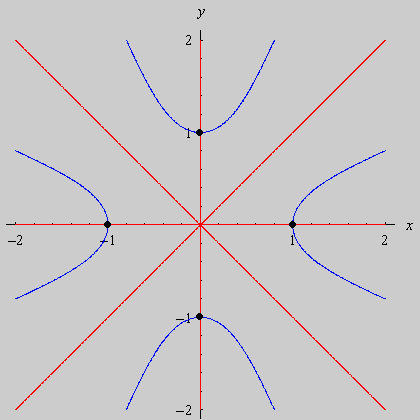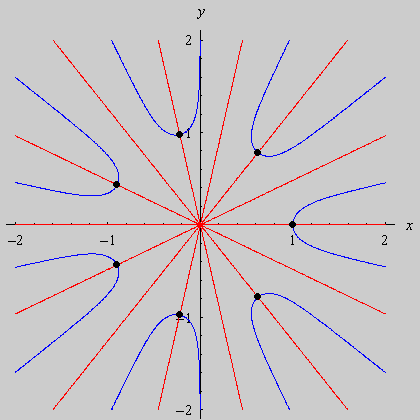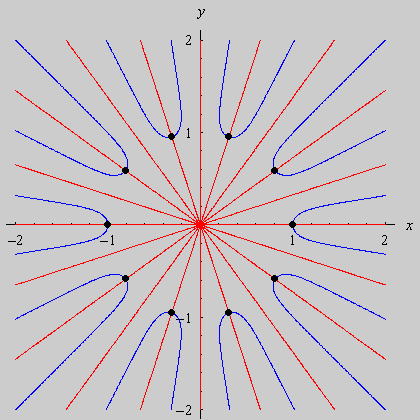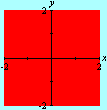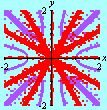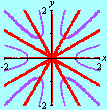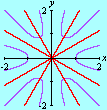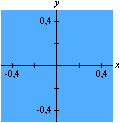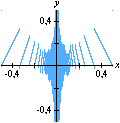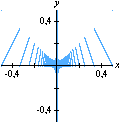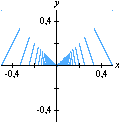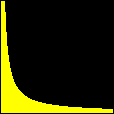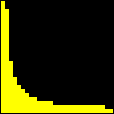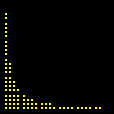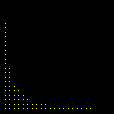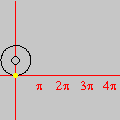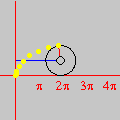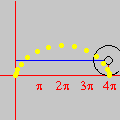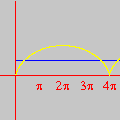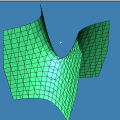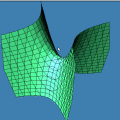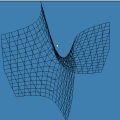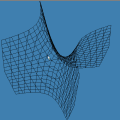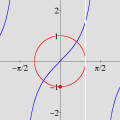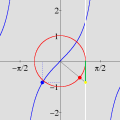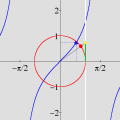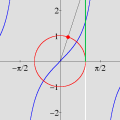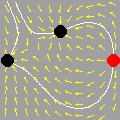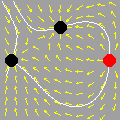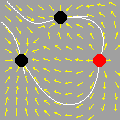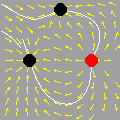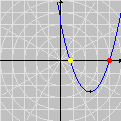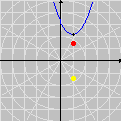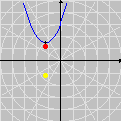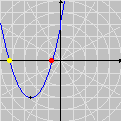Na seqüência de quadros da animação abaixo, revelamos outra maneira de se olhar para as raízes da unidade: como interseções de curvas polinomiais. De fato, a equação complexa equivale a um sistema de equações do tipo onde f e g são polinômios de grau n nas variáveis x e y. Cada uma dessas equações tem como gráfico um conjunto de curvas no plano, abaixo coloridas de vermelho e azul. As interseções dois dois conjuntos de curvas são precisamente os pontos tais que . Os quadros da nossa animação foram produzidos variando-se n de 1 até 10. (Para interromper num determinado quadro, pressione a tecla Esc; para reiniciar o filme, pressione F5.) Esta animação foi inteiramente produzida por um programa escrito por mim e rodado no Mathematica. Para cada valor de n, o algoritmo extrai as partes real e imaginária da equação , resolve o sistema, traça os gráficos respectivos, marca os pontos de interseção e salva o quadro numa pasta. Em seguida, os quadros são enfileirados com tempos de exibição definidos e reunidos num único arquivo GIF. O sistema polinomial obtido com n = 6 foi automaticamente reescrito em ASCII e colocado no GrafEq para produzir a pequena animação na qual você clicou. Carlos César de Araújo, 2 de agosto de 2002