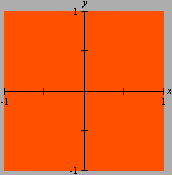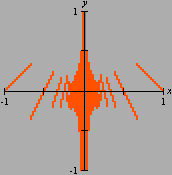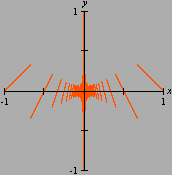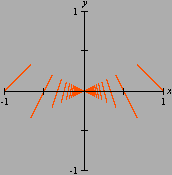
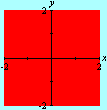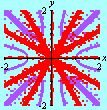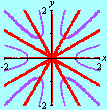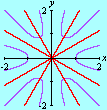
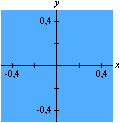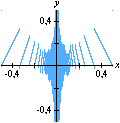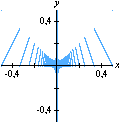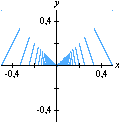
Divisões com resto O teorema fundamental da divisão inexata afirma que todo par de números naturais, com , determina um outro par de números naturais tal que e . Os números q e r são simplesmente o quociente e o resto da divisão de a por b. Quando , dizemos que a é múltiplo de b. A divisão com resto pode ser generalizada ao conjunto dos inteiros: basta manter a igualdade fundamental da divisão e exigir que o resto seja não-negativo e menor do que o módulo do divisor. Na verdade, a divisão com resto pode ser estendida ao conjunto dos números reais da mesma maneira! Essa última possibilidade é bem menos conhecida, mas torna-se menos surpreendente quando se pensa em números reais como comprimentos de segmentos da reta. 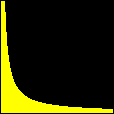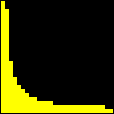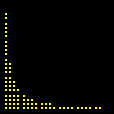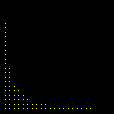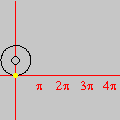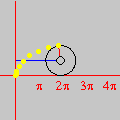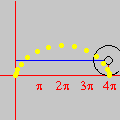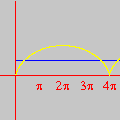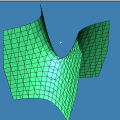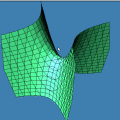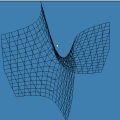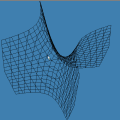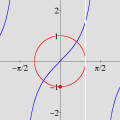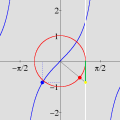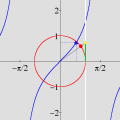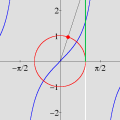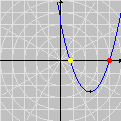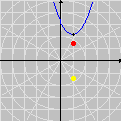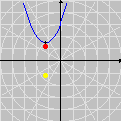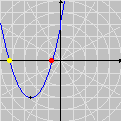A animação sobre a qual você clicou mostra o gráfico da função resto de 1 por x, sobre o intervalo . O gráfico foi produzido no GrafEq a partir da fórmula que exprime o resto generalizado em termos da função piso. A divisão inexata que vimos até agora pode ser chamada de euclidiana. Esse adjetivo torna-se necessário quando percebemos que outros tipos de "divisão com resto" são possíveis, interessantes e úteis. Dentre essas formas alternativas, a divisão com resto absoluto mínimo é especialmente importante. A animação abaixo mostra as etapas sucessivas da produção do gráfico da função resto absoluto mínimo de 1 por x no GrafEq. Para produzir o gráfico acima, utilizamos uma fórmula que calcula o resto absoluto mínimo em termos da função piso. Carlos César de Araújo, 6 de agosto de 2002