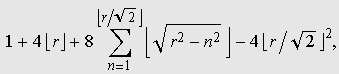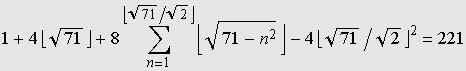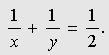Counting Lattice Points with GrafEq By Carlos César de Araújo - cca@gregosetroianos.mat.br  Portuguese version (with different examples) We will see on this page how to use GrafEq to count lattice points (i.e., points with integer coordinates) in certain subsets of . Let us first consider a disk . It is not dificult to show that the number of lattice points in this region is given by where is the floor of r. Thus there are pairs such that . 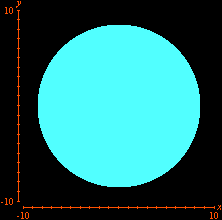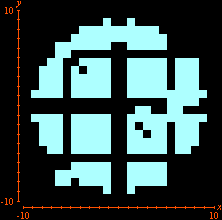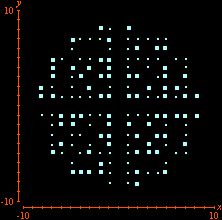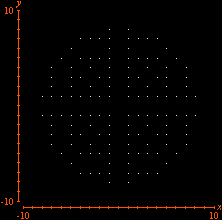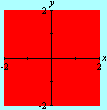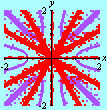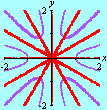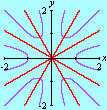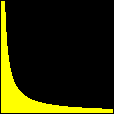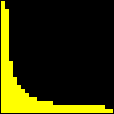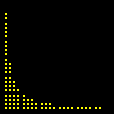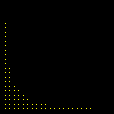We can use GrafEq to visualize this result. All we have to do is to enter with the appropriate set of relations in the algebraic relation window. Equational conditions that characterizes the set are easy to discover; two of them are and . The animation below shows the scanning process used by GrafEq to select the lattice points. You can check that the last frame ends with 221 points. 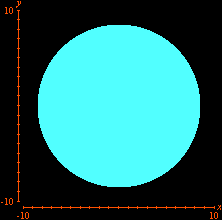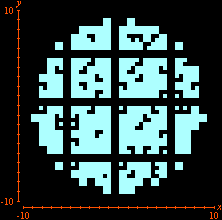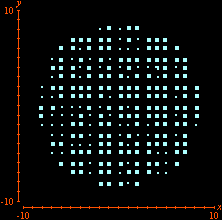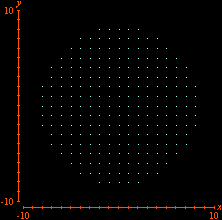(Press the Escape key to stop the GIF animation.) Additional constraints can also be included. Below we see the selection of points in the previous disk for which x and y are relatively prime. 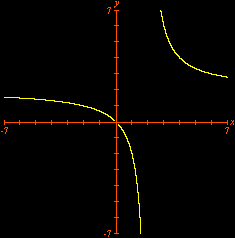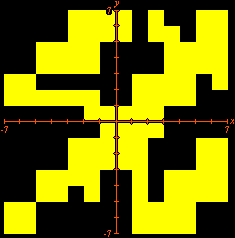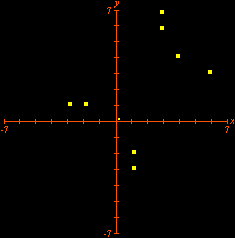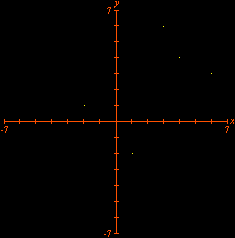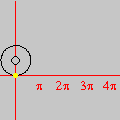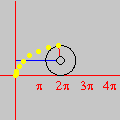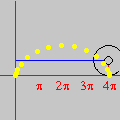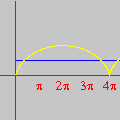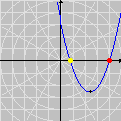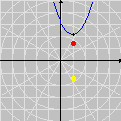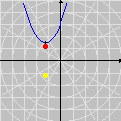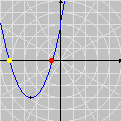This time we are left with lattice points. The real answer, nevertheless, is 136. GrafEq missed the points . What happened? This has to do with the current implementation of gcd in GrafEq 2.11 (the latest version), according to which is undefined if . Jeff Tupper will fix this behavior in a future release. Looking for lattice points in curves is the subject of Diophantine equations. The next animation shows how GrafEq detects the integer solutions to the equation The graph reveals five lattice points on the hyperbola, namely, . (Of course, the point must be excluded.) It is not difficult to prove that these are the only integer solutions. Carlos César de Araújo,  August 12, 2002