NOVAS TURMAS EM DEZEMBRO E JANEIRO! CURSO básico Pelo autor de Matemática para Gregos & Troianos APOIO e REALIZAÇÃO   Professor: Carlos César de Araújo — o matemático que revelou o Winplot ao Brasil trabalhando em contato permanente com Richard Parrris desde 1998. Público Principal: Professores do Ensino Médio. Público Secundário: Qualquer pessoa que possua bagagem matemática equivalente ou superior. Pré-requisitos: Além dos conhecimentos de Matemática pressupostos acima, o participante deve possuir familiaridade básica com teclado e mouse. Carga Horária: Doze (12) aulas, divididas em quatro (4) encontros com três (3) horas de duração cada. Dias: Sábados, às 9:00 h. Local: Colégio Arnaldinum — Rua Vitório Marçola 360, Bairro Cruzeiro Início: Aguardem confirmação para novas turmas. Preço: R$ 98,00. Certificados de Conclusão: Serão emitidos pela Informar Educacional. Locais de Inscrição Informar Educacional — Av. Afonso Pena, 3355, 11o andar - Funcionários. Telefax: (31) 3227 5766. Falar com Beth. RESUMO DOS TÓPICOS A SEREM COBERTOS Introdução ao ambiente 2D do Winplot. Os Fundamentos da Geometria Analítica As Funções Matemáticas Fundamentais (incluindo piso e teto) Programando funções Análise e ajuste de gráficos (incluindo controle de zoom, escalas, fontes, cores, estilos, etc) Equações cartesianas explícitas e implícitas Estudo da reta Estudo das cônicas Parametrização de curvas planas Técnicas de animação (constantes dinâmicas, trajetórias, etc) Transformações Geométricas (translação, rotação e homotetia) Construção de cenários Estudo completo do trinômio do segundo grau Resolução de problemas de vestibular Cenários em Trigonometria O sistema polar   Introdução ao Cálculo Diferencial (tangentes, normais, máximos e mínimos) Cálculo Vetorial no plano Aplicações à Física (simulação de experimentos físicos clássicos) 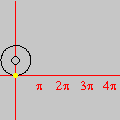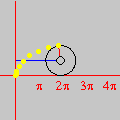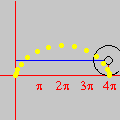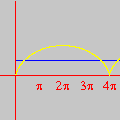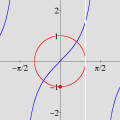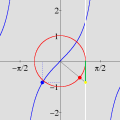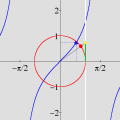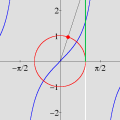OBJETIVOS DO CURSO O curso não visa apenas ensinar o domínio da interface de um software (onde encontrar menus e botões, como imprimir, etc.), contrariamente aos cursos tradicionais de "informática" no Brasil. Conforme se pode depreender da lista de tópicos, várias questões matemáticas serão abordadas, incluindo temas que normalmente não constam da formação dos professores do Ensino Médio. Portanto, ao final do curso, os professores estarão de posse não apenas um valioso instrumento tecnológico para a aceleração do aprendizado (dos alunos e dele próprio), mas contarão também com um aumento substancial dos seus conhecimentos matemáticos — sem o qual pouco poderão fazer além dos seus próprios estudantes. Um ponto importante a salientar é que a utilização efetiva (rápida e eficiente) de softwares matemáticos em salas de aula pode exigir do professor conhecimentos matemáticos que vão além das atividades elementares que ele tenciona realizar. Por exemplo, durante uma aula pode ser necessário traçar uma circunferência para algum propósito. Uma forma rápida e flexível de se obter circunferências (e curvas em geral) consiste em entrar com suas equações paramétricas. Isto não significa que, para esse fim, os alunos tenham que saber parametrização de curvas. Esse conhecimento matemático do professor é algo que ficará "por trás dos bastidores", sem ser mencionado durante a exposição, exceto se o tema da aula o exigir. Por outro lado, a espantosa evolução dos softwares nas duas últimas décadas, e a sua ampla disponibilidade em PCs, têm alterado radicalmente o quadro da educação matemática em todo o mundo. Tópicos que antes eram considerados difíceis repentinamente se tornaram imediatamente acessíveis a todos, graças ao ambiente interativo que é propiciado pelo computador. O caso das equações paramétricas é típico. Tais equações raramente eram ensinadas antes da universidade, dado o tempo necessário para se fazer entender que uma curva pode ser obtida variando-se um parâmetro num par de equações. Com os recursos de um software como o Winplot, porém, qualquer aluno que já domine o plano cartesiano estará em condições de compreender, no decurso de uma aula (!!), o importante conceito de parametrização. Tais alunos estarão numa posição privilegiada em relação àqueles que almejam cursar uma universidade dispondo apenas dos conhecimentos tradicionais. Ao longo do curso, os professores também receberão inúmeras sugestões de como propor atividades para os alunos com base no software, quer durante as suas aulas ou como deveres de casa para os seus alunos. Como exemplo, considere o estudo da equação da reta e a influência dos seus coeficientes sobre a mesma. Numa aula inicial, o professor pode instruir os alunos para que, utilizando o computador, façam descobertas mediante perguntas apropriadas. O que acontece quando o coeficiente angular é positivo? E se for negativo? Variando o coeficiente linear, o que vocês podem constatar? Indubitavelmente, o grau de participação e envolvimento dos alunos será infinitamente superior ao de uma aula comum — onde o aluno é passivamente doutrinado a adquirir técnicas sem qualquer estímulo criativo. Em resumo, esperamos que o curso proporcione aos professores uma oportunidade para que solidifiquem e enriqueçam os seus conhecimentos e, com isso, busquem uma formação acadêmica mais completa. Carlos César de Araújo, 29 de novembro de 2002