Condecorações / Awards
|
Visualizando Superfícies ImplícitasCarlos César de Araújo - cca@gregosetroianos.mat.br Um método comum para se descobrir a forma de uma superfície descrita por uma equação cartesiana implícita
consiste em examinar suas interseções com planos paralelos aos planos coordenados x y, x z e y z. Essas interseções são curvas planas que, uma vez reunidas, formam uma rede no espaço, dando-nos uma visão global da superfície. Este é um tópico constante dos cursos iniciais de Cálculo e Geometria Analítica numa universidade. Com o auxílio de figuras e animações feitas por computador, é possível acelerar formidavelmente o entendimento dessas questões, conforme mostraremos nesta página por meio de applets Java produzidos com o
LiveGraphics3D
É preciso ressaltar que nem toda equação implícita concebível
Esta condição define uma superfície. Isto é, o conjunto de todos os pontos
A eliminação de z nos dá a equação
Analogamente, quando seccionamos a superfície
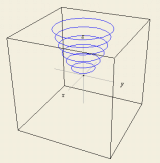
Finalmente, as seções da nossa superfície por planos Clique no botão abaixo para abrir um applet animado que mostra o traçado sucessivo de algumas seções da superfície nas três direções mencionadas. O filme deixa de rodar quando o cursor sai da região do applet. Para interromper a animação com o cursor sobre a mesma, dê um duplo-clique com o botão esquerdo do mouse. (Faça o mesmo para reiniciar.)
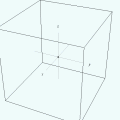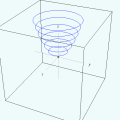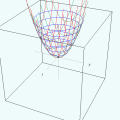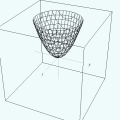
Você já consegue prever a forma da nossa superfície? O applet seguinte mostra os três conjuntos de curvas em sucessão. Além de interromper a animação, você pode "navegar" em torno da malha de curvas utilizando o mouse (pressione o botão esquerdo e arraste). Para se aproximar ou se afastar da cena, pressione SHIFT enquanto arrasta na vertical.
Se, na discussão acima, variarmos o parâmetro h de maneira contínua em cada direção, o entrelaçado de curvas se tornará uma "película" fina curvada, que é a superfície
O que você vê nessa animação é apenas parte de uma superfície ilimitada, chamada parabolóide circular. Outra denominação, mais costumeira, é parabolóide de revolução. De fato, esse tipo de parabolóide pode ser gerado pela rotação de um arco parabólico em torno do eixo O z — sendo, portanto, uma superfície de revolução. O próximo applet animado ilustra essa lei de geração, cuja descrição matemática conduz às equações paramétricas retangulares da mesma superfície. (Veja o artigo Introdução às Rotações, na seção Laboratórios.)
Para encerrar, mencionamos que o Winplot gera superfícies implícitas somente após a produção de seções transversais nas três direções principais, o que torna lenta e difícil a movimentação desse tipo de gráfico nesse software. Dos softwares apresentados neste site, o DPGraph é o que melhor produz superfícies implícitas (com base nas funções matemáticas que dispõe). Carlos César de Araújo, 12 de setembro de 2002 |
|






 . (A programação das cenas no
. (A programação das cenas no 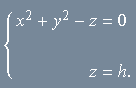
 .
.