Esferas em Espaços Métricos Uma das primeiras coisas que se aprende num curso (universitário) de espaços métricos é que existe uma infinidade de "distâncias" (ou métricas) diferentes no plano e no espaço. Uma família bem conhecida de distâncias no é a que provém das normas onde p é um número real no mínimo igual a 1. 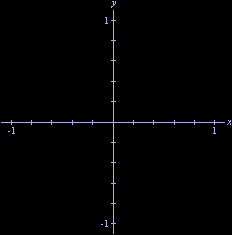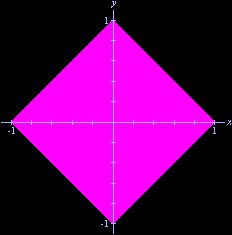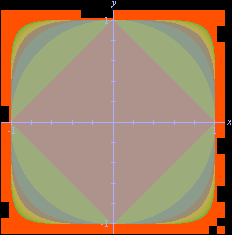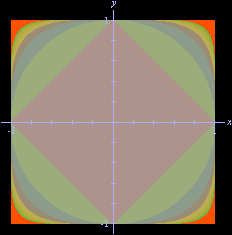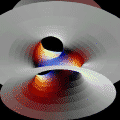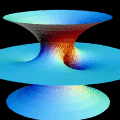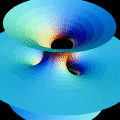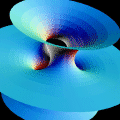Ou seja, se na conhecida fórmula da distância entre pontos do espaço tridimensional substituirmos o índice da raiz por p, e os quadrados das diferenças pelas p-ésimas potências dos módulos dessas diferenças, teremos ainda uma função que se comporta, em essência, como a distância usual (que, incidentalmente, corresponde ao caso ). Uma vez definida uma dessas distâncias, podemos fazer geometria com a mesma. Em particular, podemos falar em "esferas" (com relação à função distância escolhida). A animação (coluna direita) que conduziu a esta página ilustra o crescimento das esferas concêntricas de raio 1 , com p variando de 1 (um octaedro) até 7 e terminando com o caso limite (um cubo), sendo que . (A animação foi feita com o DPGraph.) O fato dessas esferas crescerem com p decorre das desigualdades entre normas . A discussão acima se aplica a qualquer espaço euclidiano . No caso do , o familiar plano cartesiano, mostramos o crescimento das "esferas" unitárias com p através da animação abaixo, cujos quadros foram produzidos no GrafEq. Mais precisamente, a animação mostra o crescimento das bolas (regiões planas) correspondentes às esferas (que neste caso são curvas planas). Exercício Em sua versão atual, o DPGraph não possui uma função para calcular o maior de dois ou três números dados. (O GrafEq, por outro lado, traz essa função em sua biblioteca básica — e com um número qualquer de argumentos!) Como foi então que conseguimos produzir a esfera (um cubo) no DPgraph? Uma solução para este problema consiste em exprimir a função em termos do valor absoluto (existente em quase todo software). Descubra como fazer isso. Carlos César de Araújo, 3 de outubro de 2002