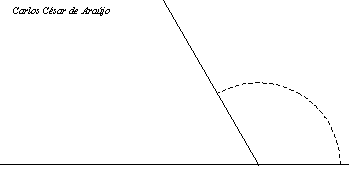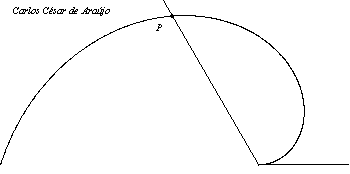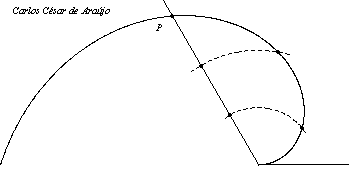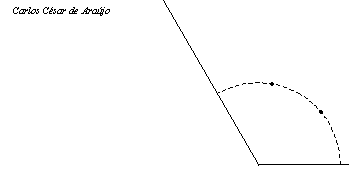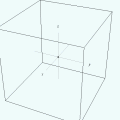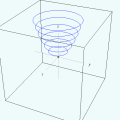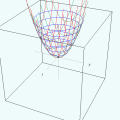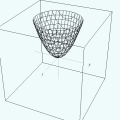
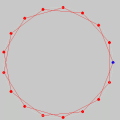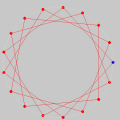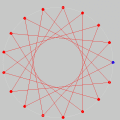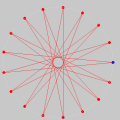
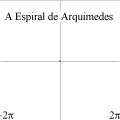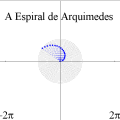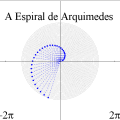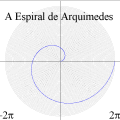
A Espiral de Arquimedes Considere um ponto em movimento retilíneo e uniforme (i.e., com velocidade constante). Agora, imagine que, ao mesmo tempo em que o ponto se desloca em linha reta, ele sofre uma rotação no sentido anti-horário (em relação à posição de partida) de um ângulo proporcional à distância percorrida. Nesse caso, a trajetória do ponto — que antes era uma reta — passará a ser uma curva em espiral, chamada espiral de Arquimedes. Ilustramos a situação com o pequeno filme abaixo, onde se vêem três pontos em movimento: um em linha reta com velocidade constante (vermelho) para a direita; outro em movimento circular uniforme (cinza claro) no sentido anti-horário; e um terceiro sob a ação simultânea desses dois movimentos (MRU e rotação anti-horária). Como em todas as animações cíclicas deste site, é necessário treinar os olhos observando a cena algumas vezes até que se compreenda o roteiro (começo e fim). No caso abaixo, procure manter os olhos em torno do centro da cena para "suavizar" a percepção dos movimentos. A tecla ESC interrompe a animação e a tecla F5 "rebobina" o filme. (Na verdade, recarrega a página.) A espiral de Arquimedes é a trajetória do terceiro ponto (de cor azul). A animação acima foi produzida no Winplot com as equações paramétricas de uma espiral de Arquimedes, as quais podem ser obtidas facilmente da descrição cinemática que demos. A trajetória do ponto em MRU sobre o eixo x consiste de todos os pares , com . Após ser submetido a uma rotação anti-horária de ângulo t, a posição do ponto será . Colocando essas equações no Winplot, você estará em condições de explorar a espiral de Arquimedes de várias maneiras; basta ter imaginação e ... conhecimento! (Veja o artigo Introdução às Rotações na seção Laboratórios.) A espiral de Arquimedes possui conexões com vários tópicos. Por exemplo, a parte da espiral correspondente a nos dá o conjunto dos números complexos que têm módulo e argumento iguais. Mas isto é uma visão moderna, e de pouca importância quando comparada às descobertas sobre a espiral feitas pelo próprio Arquimedes. Ele deu um método para traçar tangentes à espiral — que assim se tornou a primeira curva depois da circunferência a ter suas tangentes conhecidas. Mostrou que, com a ajuda da espiral, fica fácil dividir qualquer ângulo em três partes iguais (o que se provaria ser impossível, em geral, apenas com régua e compasso). Para uma apresentação desses temas (incluindo a dedução da equação polar da espiral a partir da sua definição cinemática), veja o último capítulo do CD Números . Essas e muitas outras investigações de Arquimedes foram registradas na obra Sobre espirais. No seu livro História da Matemática (Edgard Blücher, trad. de Elza Gomide), Carl Boyer observa que essa obra "foi muito admirada mas pouco lida, pois era geralmente considerada a mais difícil obra de Arquimedes." Carlos César de Araújo, 26 de setembro de 2002