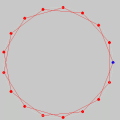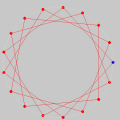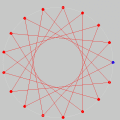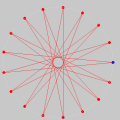
Polígonos Estrelados O estudo dos polígonos estrelados permite a exploração de fascinantes conexões entre a Teoria dos Números e a Geometria. Mas o que é um polígono estrelado? Bem, é mais fácil descrevermos como se constroem tais polígonos do que partirmos de uma definição rigorosa. Por exemplo, se dividirmos uma circunferência em 5 partes iguais e ligarmos os pontos de divisão consecutivamente, andando sempre num mesmo sentido, obteremos um pentágono regular. Mas se percorremos a circunferência ligando os 5 pontos de dois em dois, formaremos um pentágono (regular) estrelado após duas voltas. Clique no botão abaixo para ver uma animação que ilustra essa construção. O ponto azul percorre a circunferência no sentido anti-horário ligando os pontos de 2 em 2. Se ligarmos os 5 pontos de 3 em 3, obteremos o mesmo pentágono estrelado. Não obtemos um pentágono estrelado se unirmos os pontos de 4 em 4. Verifique isso. É fácil ver que, em geral, se dividirmos uma circunferência em n partes iguais e ligarmos os pontos de divisão de p em p, terminaremos com o mesmo tipo de polígono que resulta da união dos pontos de em . Exercício Após quantas voltas chegamos ao ponto de partida no caso geral? (Responda em função de n e p.) No caso particular acima, obtemos um pentágono regular comum se ligarmos os 5 pontos de 1 em 1 ou de 4 em 4; e obtemos o mesmo pentágono estrelado se ligarmos os pontos de 2 em 2 ou de 3 em 3. Segue-se que, ao investigarmos o tipo de polígono resultante da união dos n pontos de p em p, podemos nos restringir ao caso em que . Observe que ao ligarmos os n pontos de p em p, nem sempre obtemos um polígono estrelado. Exemplificando, como quer que liguemos pontos de uma circunferência de p em p (com ), jamais obtemos um hexágono estrelado. Após alguma experimentação, podemos construir uma tabela que forneça para cada os valores de p que produzem polígonos estrelados. Clique no botão abaixo para ver uma pequena tabela. Nossa tabela mostra que quando , obtemos pentadecágonos estrelados apenas para . O próximo botão abre uma animação Java que mostra esses três pentadecágonos. Os sete heptadecágonos estrelados se encontram na pequena animação da coluna direita. Tudo isso nos leva à pergunta óbvia: que relação deve existir entre n e p para que a união de n pontos de p em p nos dê um polígono estrelado de n lados? A resposta se encontra no CD Números da coleção Matemática para Gregos & Troianos. Talvez desperte o interesse do leitor saber que a produção das ilustrações desta página envolveu alguns conhecimentos de Geometria Analítica. Realmente, as figuras — pontos, segmentos e a circunferência — foram construídas tendo como pano de fundo um sistema de eixos cartesianos. Os pontos que dividem a circunferência em n partes iguais foram obtidos da expressão variando-se k de 1 a . No plano complexo, tais pontos correspondem às raízes da unidade. Toda a programação (incluindo a tabela) foi feita no Mathematica. Com os recursos do LiveGraphics3D, o código foi utilizado para produzir o applet Java do pentadecágono estrelado. No caso do applet foi necessário usar o mesmo truque do DPGraph: a figura plana foi criada no espaço cartesiano e depois colocada para ser vista de cima! Isto porque o LiveGraphics3D só produz applets de objetos gráficos tridimensionais (como o próprio " 3D" indica). Como curiosidade, mostramos abaixo o applet que contém os três pentadecágonos estrelados mergulhados no . O melhor contexto para se estudar os polígonos estrelados é a Teoria dos Grafos, normalmente ensinada em cursos de Matemática Discreta numa universidade. Além de polígonos, existem também os poliedros estrelados, sobre os quais falaremos em outra ocasião. Carlos César de Araújo, 16 de setembro de 2002