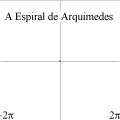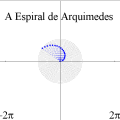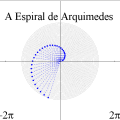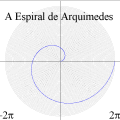
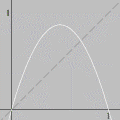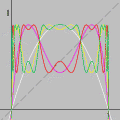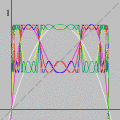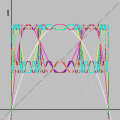
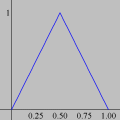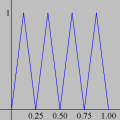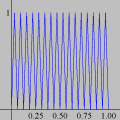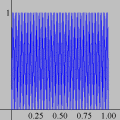
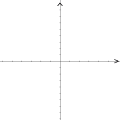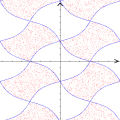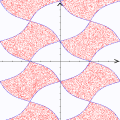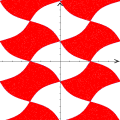
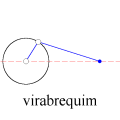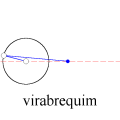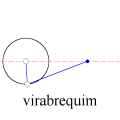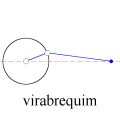
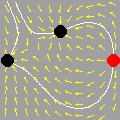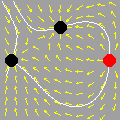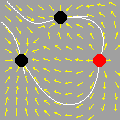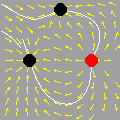
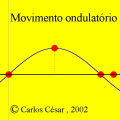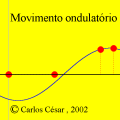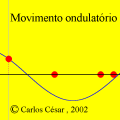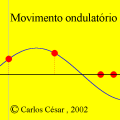
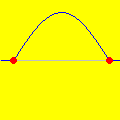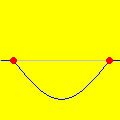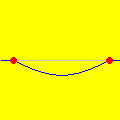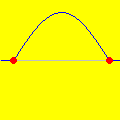
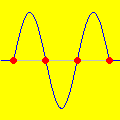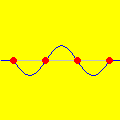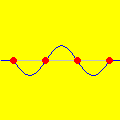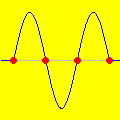
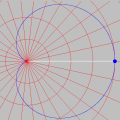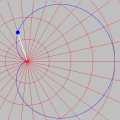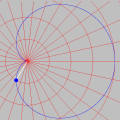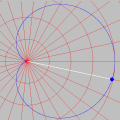
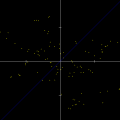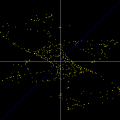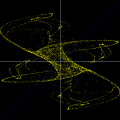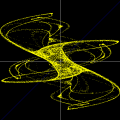
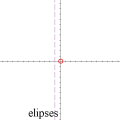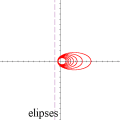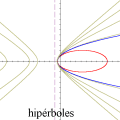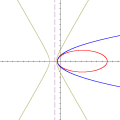
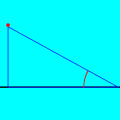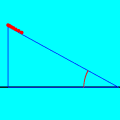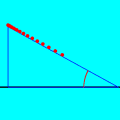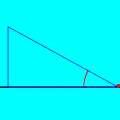
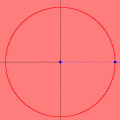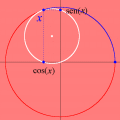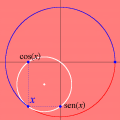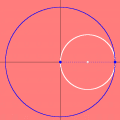
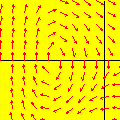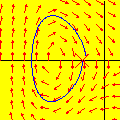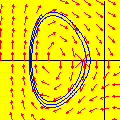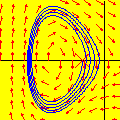
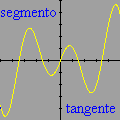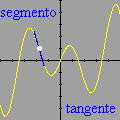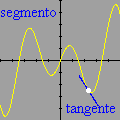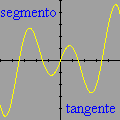
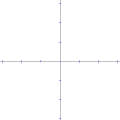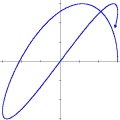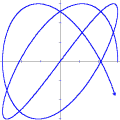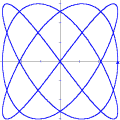
Na Onda com o Winplot Você conhece a matemática das ondas? Se o assunto alguma vez lhe pareceu trivial, retome-o com o Winplot para testar seus conhecimentos. Talvez venha a descobrir que não sabia tanto quanto pensava. Mas se esta parte da Física lhe dá dores de cabeça, o Winplot também pode ser um excelente remédio. A animação que abriu esta página mostra como seria o deslocamento de uma onda transversal numa corda fictícia (infinita e totalmente flexível). À medida que a onda se propaga para a direita, cada ponto da corda se desloca verticalmente, para cima e para baixo. Assim, após colocarmos a onda adequadamente no plano cartesiano, podemos dizer que as abscissas dos pontos não mudam. Uma vez compreendida essa questão, surge naturalmente a pergunta: fixado um ponto de abscissa x sobre a corda, como a sua ordenada y varia com o tempo? Esse deslocamento transversal deve ser especificado em termos de duas variáveis, a abscissa x e o instante t, de modo que podemos designá-lo por . A nossa pergunta pede uma "fórmula" para . A dedução matemática dessa fórmula é um pouco complicada — envolve a resolução de uma equação diferencial parcial, tópico que se vê numa universidade —, mas a resposta é comparativamente simples e pode ser apresentada de várias maneiras. 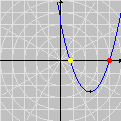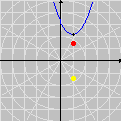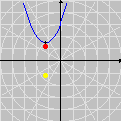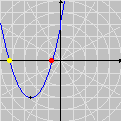Uma delas é que onde Foi basicamente esta equação que utilizamos para montar a animação no Winplot (o movimento progressivo da onda e as oscilações provocadas nos três pontos). Exceto pelo emprego adicional de funções características para controlar o movimento dos pontos vermelhos e seus traços, a única alteração que fizemos foi nas letras para as grandezas envolvidas: como o Winplot não reconhece letras gregas como constantes (apenas como texto), o segundo membro foi reescrito como a sin [2pi(x / c - t / p)] Esta pequena mudança notacional é insignificante quando comparada à fantástica compreensão que se adquire com os vários recursos dinâmicos do Winplot. É um novo mundo que se abre, totalmente diferente daquele que vemos nos livros didáticos. Ficará fácil entender os papéis desempenhados por cada uma das quantidades observando as mudanças que acarretam nos gráficos montados com o seu próprio esforço. Experimente! O que dissemos acima constitui apenas um primeiro passo. O resto fica a cargo da sua imaginação. Com o Winplot, você poderá examinar outros fenômenos ondulatórios, tais como ondas estacionárias, interferência de ondas, ressonância etc. Você ficará surpreso ao descobrir que aquelas equações estáticas realmente descrevem movimentos! 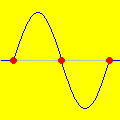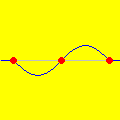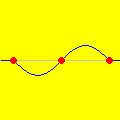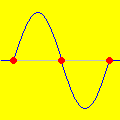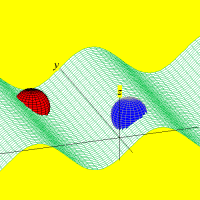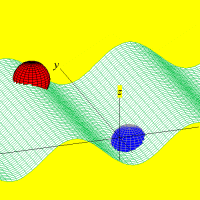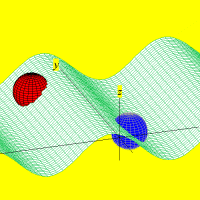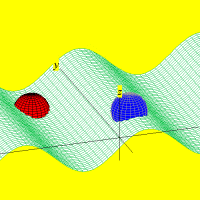Ondas estacionárias produzidas no Winplot A possibilidade de animar equações no computador lança um novo sopro de vida ao conhecimento armazenado nos livros. Sim, aqui continua valendo o nosso velho lema: a imaginação não é nada sem o conhecimento. 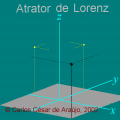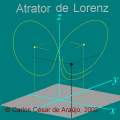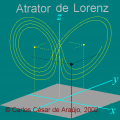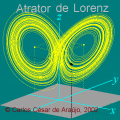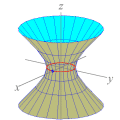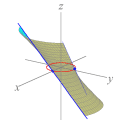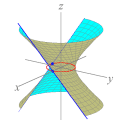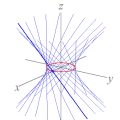Onda tridimensional obtida de y=a*sin[2pi(x/c-t/p)] Carlos César de Araújo, 29 de novembro de 2002