A igualdade (8)
![]() ,
,
vista há pouco, nos dá uma demonstração e, ao mesmo tempo, uma reformulação da Regra de Cramer. O ponto de partida é o sistema
![]()
tal como anteriormente. Se multiplicarmos à esquerda os dois membros por ![]() e usarmos a igualdade (8), teremos
e usarmos a igualdade (8), teremos
![]()
ou
![]()
Agora, basta um pequeno instante de reflexão para perceber que o sistema (9) é o mesmo sistema (7) que discutimos antes. A única diferença é que os determinantes de Cramer
![]() do sistema (7) aparecem em (9) desenvolvidos em relação aos cofatores da coluna
do sistema (7) aparecem em (9) desenvolvidos em relação aos cofatores da coluna ![]() . Mais precisamente,
. Mais precisamente,
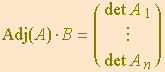 .
.
Se ![]() , então podemos concluir de (9) que
, então podemos concluir de (9) que
![]()
Eis aí, em essência, a “Regra de Cramer”.
A vantagem de (9) é que ela nos permite ver mais claramente onde está o erro da condição (T2) do nosso equivocado teste. Pelo fato de termos obtido o sistema (9) multiplicando o sistema
![]() pela matriz
pela matriz ![]() , fica evidente que esses sistemas não são, em geral, equivalentes (a menos que a adjunta seja inversível). Em particular, vejamos novamente o que acontece quando
, fica evidente que esses sistemas não são, em geral, equivalentes (a menos que a adjunta seja inversível). Em particular, vejamos novamente o que acontece quando
![]()
Isto é o mesmo que dizer que
![]()
Neste caso, portanto, vamos do sistema ![]() ao sistema
ao sistema ![]() (onde
(onde ![]() é a matriz nula). A multiplicação pela adjunta de
é a matriz nula). A multiplicação pela adjunta de ![]() , neste caso, “destrói” completamente o sistema original! Claramente, o sistema
, neste caso, “destrói” completamente o sistema original! Claramente, o sistema
![]() possui infinitas soluções, mas daqui não se pode concluir o mesmo quanto a
possui infinitas soluções, mas daqui não se pode concluir o mesmo quanto a
![]() .
.
Exercício 2
Mostre que os sistemas ![]() e (9) são equivalentes quando
e (9) são equivalentes quando ![]() .
.