Relembrada a Regra de Cramer, passemos ao enunciado do falso resultado que anunciamos na Introdução. Mas antes, tenhamos em mente as duas questões fundamentais que surgem quando se está envolvido com a resolução de equações em geral. No nosso caso, a primeira delas é simplesmente esta:
Quantas soluções reais possui um sistema linear 
?
Estamos supondo que os coeficientes e os termos constantes do sistema são números reais arbitrários. Neste caso, o universo numérico mais vasto é 
. Cada solução do sistema é uma 
-upla ordenada de números reais. Perguntamos: quantas 
-uplas de números reais podem ser soluções do sistema?
Resumidamente, a resposta é: nenhuma, uma ou infinitas. Estas são as três única opções possíveis em 
. Colocamo-las no quadro abaixo juntamente com as suas denominações tradicionais.
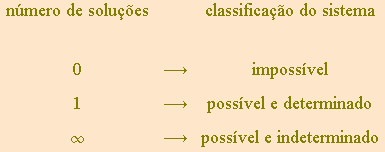
O sinal “
” é o famoso “símbolo de infinito”. Usamo-lo aqui como um número
cardinal para indicar uma infinidade de soluções.
Parece-me indubitável que o raciocínio matemático se torna mais ágil quando substituímos longas descrições verbais por formulações simbólicas compactas, claras e naturais. Assim, em vez de repetirmos a todo instante as frases longas
“impossível”, “possível e determinado” e “possível e indeterminado”,
adquirimos maior controle da situação quando percebemos que estamos simplesmente discutindo as possibilidades
“zero”, “um” e “infinito”
quanto ao número de soluções reais de um sistema de equações. Estamos meramente discutindo a cardinalidade do conjunto-solução de uma equação da forma 
, em que 
e 
são matrizes (de números) reais, sendo 
quadrada. Se quiséssemos indicar esse número cardinal por um símbolo, digamos
então poderíamos ter dito apenas:
A segunda questão que se coloca é: como decidir, na prática, qual dessas três possibilidades ocorre?
É como uma resposta a esta segunda questão que se propôs o falso teste baseado na Regra de Cramer. Vamos enunciá-lo na próxima página.