Voltemos ao caso dos sistemas 
em que 
é uma matriz quadrada de ordem
. Utilizaremos o Teorema de Rouché para mostrar como fortalecer as condições
a fim de que se possa concluir que o sistema é indeterminado. Eis o resultado:
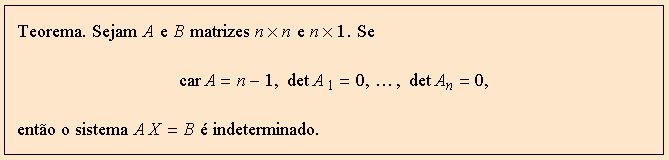
Observe que o enunciado desse teorema difere da condição (T2) somente pelo fato de “
” ter sido substituído por
“
”.
Isto é, a condição sobre o determinante da matriz A foi substituída
por uma restrição mais forte sobre a sua característica. O teorema acima
aparece como parte do Teorema 19 (p. 981) da referência [2], embora seja
formulado diferentemente e sem nenhuma conexão com o tipo de erro que ora
discutimos.
Exemplo 7
Para o sistema do primeiro contra-exemplo, temos 
. Se fosse 
, então, pelo teorema que acabamos de provar, aquele sistema teria uma infinidade de soluções. Mas um argumento simples nos mostrou que o sistema é impossível. Só resta concluir, portanto, que 
conclusão que havíamos obtido por cálculo direto no
Exemplo 6.
Exercício 6
Prove que a condição 
é realmente mais forte do que
.
Exercício 7
Prove que para 
e 
, as condições
implicam que o sistema
é indeterminado.