Contrariamente ao que se afirma em muitos trabalhos didáticos publicados no Brasil, a nulidade dos determinantes da Regra de Cramer, isto é, as condições
não são suficientes para garantir que um sistema linear de 
equações a
incógnitas 
seja indeterminado. Usando o Teorema de Rouché, mostramos que essas condições acarretam a indeterminação do sistema nos casos em que (a) 
ou (b) 
e 
. Mas as condições não têm força suficiente para garantir a indeterminação em todos os casos, conforme mostramos mediante um contra-exemplo simples. Por outro lado, uma outra aplicação do Teorema de Rouché nos fez ver que as condições
implicam a indeterminação do sistema em todos os casos.
Em resumo, podemos dizer que provamos o seguinte:
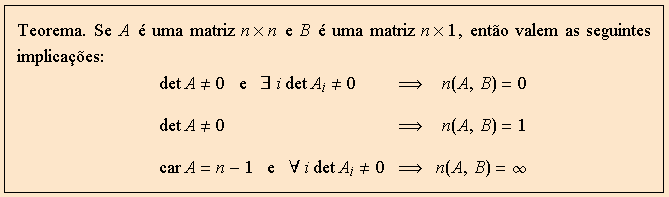
Mas é importante ressaltar que este resultado é de pouco valor prático. Nenhum critério que dependa do cálculo de muitos determinantes pode ser considerado “prático”. Além disso, ao contrário do que ocorre com o Teorema de Rouché, as hipóteses do teorema acima não são exaustivas, conforme ilustramos abaixo:
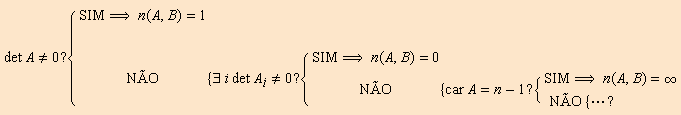
A conclusão após o último NÃO tanto pode ser “
” como
“
”. Exemplos? Deixamos aos cuidados do leitor como exercício.