Fiz questão de apresentar um contra-exemplo tirado de uma publicação conhecida ([6]) para mostrar que um mínimo de apego à farta literatura existente seria suficiente para impedir que os autores brasileiros (ou de qualquer canto do orbe) cometessem um erro tão ingênuo. Resta saber o que os teria levado a tirar uma conclusão visivelmente falsa da Regra de Cramer. Para isto, teremos que examinar a própria regra em uma forma um pouco “recuada”.
O argumento clássico que conduz à Regra de Cramer é, em linhas gerais, o seguinte. Partindo de um sistema linear
,
em que 
é uma matriz 
, é possível, mediante certas transformações que examinaremos adiante, levar o sistema à forma
O que temos aqui é também um sistema linear com 
equações nas variáveis originais, só que muito mais simples, já que todas as equações são da forma 
. Podemos dizer que o sistema
foi transformado em 
, onde 
é diagonal. Para se chegar a este ponto, nenhuma hipótese especial sobre as matrizes
e 
se faz necessária. Prova-se apenas que toda solução do sistema
é solução do sistema simplificado (7), isto é:
Se , então 
é solução do sistema (7).
Naturalmente, a intenção primordial aqui é o cálculo de 
. A fim de que possamos concluir validamente de (7) que
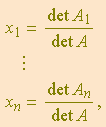
temos que assumir uma hipótese: a de que 
. Portanto, vale a seguinte implicação:
Estritamente falando, isto por si só não garante que as frações 
compõem uma solução do sistema inicial. É necessário fazer o raciocínio inverso e verificar que os candidatos assim apontados realmente satisfazem o sistema. Mas, conforme ficará claro depois, trata-se de tarefa bem fácil, de modo que podemos dar o caso
por encerrado. Com isto, provamos que a condição
(T3) é verdadeira.
Vejamos agora o que acontece com (7) se 
. Temos então dois casos a considerar: ou todos os 
são zero ou pelo menos um deles é diferente de zero.
Se
mas pelo menos um dos 
é diferente de zero, então, claramente, teremos pelo menos uma equação em (7) da forma
em que 
e 
. Mas tal equação é impossível, donde o sistema (7) também o é. Como toda solução do sistema inicial é solução de (7), a impossibilidade de (7) acarreta a impossibilidade do sistema original. Com isto provamos a
condição (T1).
Finalmente, se
e todos os
são zero, então todas as equações em (7) são da forma 
. Ora, tais equações são satisfeitas por quaisquer 
, já que 
vezes qualquer número é sempre 
. Sendo satisfeitas por todos os
, o sistema (7) possui infinitas soluções.
É aqui que tem início, creio, a origem do raciocínio falacioso que conduz à
condição (T2). Pensou-se que o sistema inicial
também deveria possuir infinitas soluções neste caso. Dissemos que toda solução do sistema
é solução de (7), mas esses dois sistemas não são equivalentes em todos os casos. As manipulações algébricas que transformam o sistema
no sistema (7) não preservam as soluções do primeiro no caso em que
e todos os
são zero.
Podemos ver mais claramente que os sistemas
e (7) nem sempre são equivalentes se reescrevermos este último numa forma mais compacta utilizando o conceito de adjunta de uma matriz. Isto será visto na página seguinte.