O conceito de “característica” se aplica a matrizes quaisquer, quadradas ou não. A característica de uma matriz é um inteiro não-negativo que é sempre menor ou igual ao número de linhas e ao número de colunas. Isto é uma propriedade do conceito, nao uma definição. A definição comum em textos pré-universitários utiliza determinantes. A formulação é a seguinte.
Se 
é a matriz nula, dizemos que a característica de
é zero. Caso contrário, dizemos que
tem característica 
quando são satisfeitas as seguintes condições:
(1) Existe pelo pelos uma submatriz 
de
cujo determinante é diferente de zero.
(2) Toda submatriz quadrada de ordem superior a 
tem determinante zero.
Um menor de uma matriz é o determinante de uma submatriz. Assim,
tem característica
quando possui pelo menos um menor de ordem
não-nulo e todo menor de ordem superior é nulo. Vamos indicar a característica de
por 
.
Para 
, podemos dizer que
é o maior inteiro não-negativo
tal que
possui pelo menos uma submatriz
com determinante não-nulo. Evidentemente,
onde 
é o número de linhas de
e 
é o número de colunas.
Exemplo 4
Suponha que
é quadrada de ordem 
. Então
De fato, se 
, então deve existir uma submatriz 
de
com determinante não-nulo. Mas a única submatriz 
de
é ela própria. Assim, 
. O raciocínio inverso é igualmente fácil.
Observe que o cálculo da característica por meio da definição acima pode ser algo laborioso. Dada uma matriz
, a fim de nos certificarmos de que 
devemos, em princípio, extrair de
todas as suas submatrizes quadradas de ordem 
ou superior e testar se o determinante de alguma delas é zero ou não. Um método muito mais eficiente consiste em escalonar a matriz, isto é, reduzi-la a uma forma “em escada” mediante operações elementares de linha. Como nossa discussão teve início com os determinantes da Regra de Cramer, não discutiremos aqui o cálculo da característica por esse método.
Embora a definição de característica em termos de determinantes seja pouco prática, cabe dizer que, em estudos matemáticos mais avançados (cf.
referência [3]) , a formação de menores (determinantes de submatrizes) tem uma certa importância
(além do seu uso no clássico “Teorema Geral de Laplace”; veja a referência
[1]). Podemos imaginar todas as submatrizes
de
dispostas num quadro com linhas e colunas segundo uma ordem natural (a ser exemplificada adiante). Se tomarmos os determinantes dessas submatrizes assim arranjadas e os colocarmos numa outra matriz, teremos formado a chamada 
-ésima potência exterior da matriz
. Essa matriz dos determinantes de todas as submatrizes
(isto é, dos menores de ordem 
) é denotada por 
.
Em geral,
é uma matriz enorme, com 
linhas e 
colunas. Para o caso em que 
, convém definir
que é a matriz 
cujo elemento é o número 1.
Com o conceito de potência exterior, a característica de uma matriz pode ser definida assim:
Exemplo 5
Para uma matriz genérica 
a matriz formada pelos determinantes de todas as suas submatrizes 
, dispostos em ordem natural, é
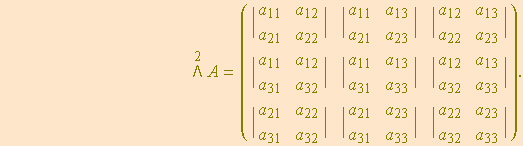
Se pelo menos um desses determinantes for não-nulo, isto é, se 
for diferente da matriz nula, então a característica de
será no mínimo 
. Neste caso, para que a característica seja exatamente 2, a matriz 
deve ser nula, isto é, 
.
Exemplo 6
Para a matriz
do contra-exemplo da condição (T2), devemos ter 
, já que 
. Mas
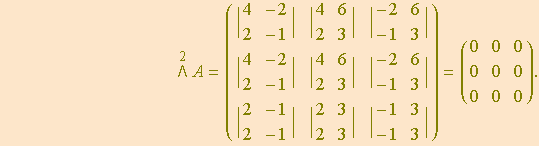
Portanto, 
.
Exercício 3
Mostre que para toda matriz quadrada
de ordem 
, tem-se
Exercício 4
Para uma matriz
, prove as seguintes implicações a partir das definições dadas até o momento:
(1) Se 
, então 
.
(2) Se 
, então 
.
Exercício 5
Sejam
e 
matrizes 
e 
, respectivamente. Forme a matriz 
, de dimensões 
, pelo acréscimo de uma coluna formada pelos elementos de
. Mostre que
onde 
são os determinantes de Cramer relativos ao sistema
. Observe que
aparece multiplicado por 
.
Finalmente, informamos que um outro termo usado em vez de “característica” é “posto”. Você ouvirá falar do posto de uma matriz se cursar uma disciplina como Álgebra Linear na universidade.