Contra-exemplo
Tomemos o sistema
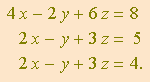
A matriz dos coeficientes é
As matrizes 
da Regra de Cramer são
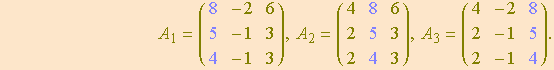
Um cálculo direto mostra que todos os respectivos determinantes são nulos:
Se o teste enunciado na página anterior fosse integralmente verdadeiro, então, de acordo com a cláusula (T2), deveríamos concluir que o número de soluções é infinito, isto é, que o sistema é indeterminado. Todavia, o número de soluções é zero! Basta examinar com mais atenção as duas últimas equações:
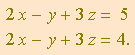
Os primeiros membros são idênticos. Logo, se existisse solução, teríamos 
, uma contradição. Estas equações são inconsistentes, o que torna impossível qualquer sistema que as contenha.
O exemplo que acabamos de dar foi tirado da referência [6] da bibliografia. Na página 311 da edição brasileira, é dito explicitamente (em outras palavras) que da nulidade de todos os determinantes de Cramer nada se pode concluir: "o sistema pode ser ou não possível". Na lista de "Problemas Resolvidos", o autor fornece (Problema Resolvido 24) o contra-exemplo que discutimos acima.