Clique no link abaixo para ver a nona questão da prova de Matemática (segunda etapa) do vestibular da UFMG de 1997. Segundo Antônio Zumpano, esta questão foi proposta em decorrência do debate que se seguiu à divulgação geral do erro que ora examinamos.
Questão (UFMG 1997)
A resolução é simples. Calculando os determinantes, encontra-se
Assim, os quatro determinantes de Cramer são simultaneamente nulos exatamente quando 
, independentemente de 
. Para esse valor de 
a matriz completa do sistema torna-se
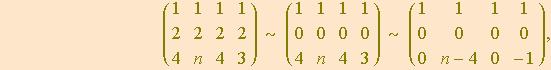
mostrando que o sistema será, neste caso, impossível se e somente se 
.
Parece-me, contudo, que a formulação do problema falhou em seu propósito de alertar o candidato para essa importante lição: os determinantes de Cramer do sistema 
cuja matriz completa é
são todos nulos (conforme mostraram os cálculos do item A), mas disso não se pode concluir que o sistema é indeterminado (como se afirma em muitos livros). De fato, os cálculos do item B mostraram que o sistema é impossível.