A chamada “Regra de Cramer” nos dá uma fórmula para resolver sistemas lineares do tipo
em termos de determinantes. A regra nos fornece instruções precisas para o cálculo das incógnitas 
em função dos coeficientes 
e dos termos 
.
Observe que o sistema acima consiste de 
equações lineares com
incógnitas 
. Assim, o número de equações é igual ao número de incógnitas. A fórmula de Cramer só se aplica a sistemas lineares dessa espécie.
Uma maneira de apresentar a Regra de Cramer, comum em textos antigos, é a seguinte:
Nesta notação arcaica, 
é o determinante do sistema (1), isto é, o determinante da matriz dos coeficientes:
Os numeradores em (2) também são determinantes, os quais se relacionam com 
da seguinte maneira:
Para cada 
de 
a
, 
é o determinante que se obtém de
substituindo-se a sua 
-ésima coluna pela coluna dos termos constantes.
Os termos constantes do sistema (1) são 
; eles não dependem das incógnitas. De acordo com o parágrafo precedente, devemos ter:
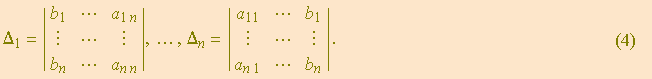
Nas páginas que se seguem, usaremos ocasionalmente o termo “determinantes de Cramer” para nos referirmos a 
em geral. Em breve daremos dois exemplos concretos de aplicação da regra.
Nos textos atuais, a notação matricial tem um papel maior. Houve época em que se falava em “teoria dos determinantes” (na tradição de Laplace, Cauchy e Gauss); as matrizes não eram mencionadas. Hoje já não se fala mais em “determinante”, mas em “determinante de uma matriz”. As matrizes estão no centro das atenções. O determinante é apenas uma função de matrizes: para cada matriz quadrada (de números reais)
, temos o número real
o determinante de . Além desta notação com barras, usaremos também
A função 
leva matrizes em números reais.
Em termos de matrizes, o sistema (1) pode ser escrito como
onde
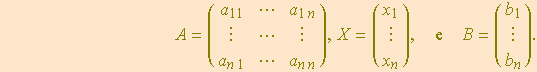
Neste contexto, tornou-se comum apresentar as igualdades (2) assim:
onde 
é a matriz que se obtém de
colocando (os elementos de) 
em sua 
-ésima coluna.
Há mais um detalhe importante sobre a Regra de Cramer: ela só se aplica a sistemas 
para os quais 
, isto é
Esta restrição torna-se evidente a partir da própria regra tal como apresentada em (2) ou em (6). Como as incógnitas são expressas por frações nas quais o determinante do sistema figura nos denominadores, é necessário supor que esse determinante seja não-nulo 
uma vez que a divisão por zero é impossível.
Em resumo, a Regra de Cramer nos diz que para toda matriz quadrada
tal que 
, o sistema
(seja qual for ) tem solução única, e esta solução é dada por
