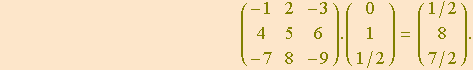Visando ilustrar a Regra de Cramer, consideremos o sistema linear 
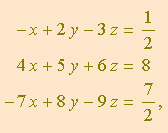
cuja matriz dos coeficientes é
Calculando o determinante, vê-se que
Como o determinante é diferente de zero, o sistema possui solução única. Para calcular a solução pela Regra de Cramer, substituímos sucessivamente as colunas da matriz 
pela matriz-coluna dos termos independentes
Isto nos leva às matrizes
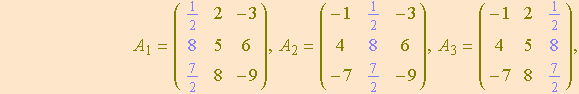
cujos determinantes são
Portanto, pela Regra de Cramer,
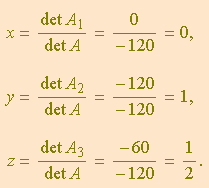
Você pode constatar que a tripla 
é, de fato, solução do sistema conferindo a igualdade
