Dado o inteiro 
, em notação decimal, consideremos uma permutação 
sobre o conjunto
Examinemos este trecho:
Dado o inteiro , em notação decimal, consideremos uma permutação sobre o conjunto
O autor pretende descrever os números 
derivados de 
por uma permutação dos algarismos. Ora, o conjunto dos algarismos de N é 
. Portanto, pela definição de "permutação" dada no artigo, permutações dos algarismos corresponderiam a bijeções
.
A idéia é que todos os números são da forma
.
Mas o plano não funcionará se N tiver algarismos repetidos.
Para 
e 
, podemos obter
números distintos por permutação da seqüência dos algarismos de N :
.
Desses 6 números, apenas 2 são da forma 
. Pois, embora N tenha 4 algarismos, o conjunto dos mesmos,
,
possui 2 elementos. Portanto, existem 
permutações do conjunto dos algarismos. São elas:
dada por 
dada por 
Se aplicarmos essas bijeções à seqüência dos algarismos de 
, obteremos 2 dos 6 números acima:
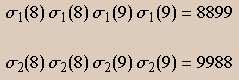
Os 4 números restantes simplesmente escaparam!
Carlos César de Araújo, 25 de agosto de 2003