Trechos do artigo
Transcrevemos, abaixo, apenas os trechos relevantes do artigo de Doherty Andrade (algumas preliminares, dois lemas e o teorema final). As partes omitidas são indicadas por "(...)". Procuramos manter os detalhes tipográficos (espaçamento, negrito, itálico, etc.) próximos do original.
(...)Uma permutação sobre um conjunto 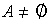 é uma bijeção de A em A.
é uma bijeção de A em A.
Dado o inteiro 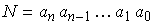 , em notação decimal, consideremos uma permutação
, em notação decimal, consideremos uma permutação 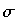 sobre o conjunto
sobre o conjunto
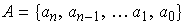
Representaremos 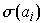 por
por 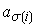 . Assim, de uma permutação dos algarismos de N, resulta um inteiro N' que, em notação decimal, se escreve
. Assim, de uma permutação dos algarismos de N, resulta um inteiro N' que, em notação decimal, se escreve
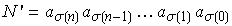 ,
,
ou seja,
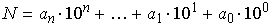
e
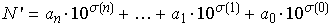
Lema 1. 9 é um divisor de 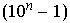 , para todo natural n.
, para todo natural n.
A demonstração pode ser feita por indução ou observando que 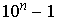 é um número constituído somente de "noves".
é um número constituído somente de "noves".
Lema 2. 9 é um divisor de 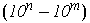 , quaisquer que sejam os naturais m e n.
, quaisquer que sejam os naturais m e n.
Para provar isto (...)
Teorema. 9 é um divisor de 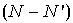 , onde N e
, onde N e 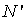 são dados como acima.
são dados como acima.
A prova é trivial. Observe que
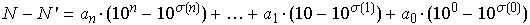 .
.
Como (...)
Extraído do artigo de Doherty Andrade O nove misterioso, RPM 9 (1986), pp.30-31.
Os lemas 1 e 2 são verdadeiros, e suas respectivas demonstrações estão corretas. Para o Teorema final, o autor mostra que a diferença 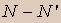 é uma soma de termos da forma
é uma soma de termos da forma 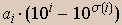 , com
, com 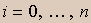 ; e como, pelo Lema 2, cada
; e como, pelo Lema 2, cada 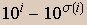 é um múltiplo de 9, fica claro que
é um múltiplo de 9, fica claro que
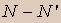 é um múltiplo de 9. Ponto final. O que há de errado com o argumento?
é um múltiplo de 9. Ponto final. O que há de errado com o argumento?
O principal ponto fraco do argumento está no começo, no preâmbulo. Se o autor tivesse escrito um programa de computador com base nas suas especificações iniciais, veria as mensagens de alerta durante a execução. Veria então que o (principal) erro não está, por assim dizer, no algoritmo, mas na estrutura dos dados. Os detalhes são apresentados nas próximas páginas.
[ Voltar ] [ Acima ] [ Avançar ]
Carlos César de Araújo,
25 de agosto de 2003
![]() é uma bijeção de A em A.
é uma bijeção de A em A.![]() , em notação decimal, consideremos uma permutação
, em notação decimal, consideremos uma permutação ![]() sobre o conjunto
sobre o conjunto
![]()
![]() por
por ![]() . Assim, de uma permutação dos algarismos de N, resulta um inteiro N' que, em notação decimal, se escreve
. Assim, de uma permutação dos algarismos de N, resulta um inteiro N' que, em notação decimal, se escreve
![]() ,
,
![]()
![]()
![]() , para todo natural n.
, para todo natural n.
![]() é um número constituído somente de "noves".
é um número constituído somente de "noves".
![]() , quaisquer que sejam os naturais m e n.
, quaisquer que sejam os naturais m e n.
![]() , onde N e
, onde N e ![]() são dados como acima.
são dados como acima.
![]() .
.