[ 1. Introdução ] [ 2. Versões alternativas ] [ 3. Comparação de cardinais ] [ 4. A heurística da demonstração ] [ 5. A demonstração ] [ 6. Referências ]

5 A demonstração

Dados um conjunto A e uma função , provaremos que

.

Para isto, seguimos o que foi visto na página anterior e definimos

.

Agora, fixado um a qualquer, mostraremos que . De fato, admitamos que

.

Então, pela própria definição de igualdade de conjuntos,

.

Em particular (tomando ),

.

Observe-se que esta sentença tem a forma :

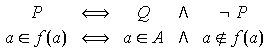
Por causa da tautologia

,

inferimos que

.

Acabamos de provar a implicação para . Como a foi arbitrário, concluímos que , isto é, que a função não é sobrejetora. Está terminada a prova do Teorema de Cantor.

[ Voltar ] [ Capa ] [ Avançar ]

Carlos César de Araújo, 27 de julho de 2003