Algarismos na base b (Parte I)
Carlos César de Araújo

Matemática para Gregos & Troianos

Para a maioria das pessoas, “números” são numerais na base 10. Agora, basta um pouco de reflexão para se convencer de que os números com algarismos são os que vão de (com zeros) a ( noves).

Esse fato tão familiar continua verdadeiro quando usamos numerais numa base diferente de 10. Nessa direção, o seguinte resultado foi provado no Capítulo VII do CD Números (link Exemplos Adicionais e Problemas Resolvidos 1-7, Exemplo 6):

Proposição 1. Sejam números naturais, com . Se possui algarismos quando escrito na base , então .

Vale também a recíproca:

Proposição 2. Sejam números naturais, com . Se , então possui algarismos quando escrito na base .

No CD Números, a Proposição 2 foi deixada como exercício, para o qual oferecemos a seguinte sugestão: “Tente provar isto efetuando divisões em escada de por ”. Alguns leitores nos escreveram dizendo que não conseguiram uma demonstração “convincente”. Vejamos onde residem as dificuldades.

Estamos afirmando que se , então, após divisões em escada por

teremos a seguinte representação de como um polinômio em de grau (isto é, )

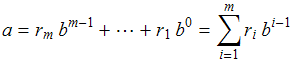
onde os coeficientes , por serem restos de divisões por , pertencem ao conjunto . As dúvidas são:

• Como podemos ter certeza de tudo isso sabendo apenas que ?
• Como podemos provar que serão necessárias exatamente divisões por ?
• Existe uma “fórmula geral” para os algarismos em função de e ?

Neste artigo, esperamos esclarecer essas e outras questões utilizando resultados dos capítulos XIX e XX do CD Números. Apresentaremos uma demonstração da Proposição 2 em duas versões, que diferem entre si no fato de a primeira ser mais verbosa e heurística do que a segunda. O argumento é basicamente o que se encontra nos textos tradicionais, mas com uma possível novidade: a representação posicional é derivada numa forma explícita em termos da função piso. Na Parte II usaremos a mesma técnica para discutir a representação posicional de números reais. Na Parte III — e retomando um tema já discutido no CD Números, mas sob uma nova luz — veremos o que acontece quando a base é negativa.

Carlos César de Araújo, 15 de abril de 2006, 14:41:33