Demonstração II
Matemática para Gregos & Troianos
Na página anterior obtivemos a representação de 
na base 
mediante substituições e expansões sucessivas. O mesmo procedimento pode ser apresentado de maneira mais elegante se usarmos a propriedade telescópica dos somatórios (veja o CD Números, Capítulo II, Somatórios, fórmula S6). Como antes, partimos da fórmula do resto euclidiano em função do piso
da qual obtemos (por substituição de 
por 
)
e (após multiplicar os dois membros por 
)
Segue-se que, para todo 
,
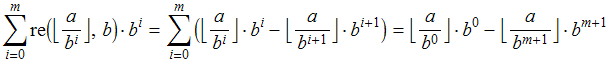
ou ainda (tendo em vista que estamos supondo 
)
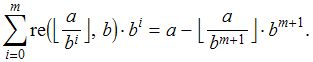
Mas provamos na página anterior que
Assim,
de modo que (fazendo 
na última soma acima)
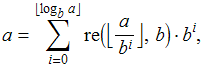
exatamente como antes.
Carlos César de Araújo, 16 de abril de 2006, 15:31:05