Demonstração I
Matemática para Gregos & Troianos
No Capítulo XX do CD Números mostramos que o resto 
da divisão de 
por 
(
) pode ser expresso por meio da função piso de acordo com a seguinte expressão:
Aqui suporemos que 
são números naturais (elementos de 
) e que 
.
Reescrevamos (1) na seguinte forma:
Esta igualdade — que simplesmente traduz a divisão “inexata” de 
por 
— é a base de todo o processo para a obtenção de uma representação posicional de 
na base 
. Note-se que em (2) já temos uma expressão polinomial em 
(de grau no máximo 1) no segundo membro. Por definição, teremos uma representação posicional na base 
com 
algarismos somente se chegarmos a um polinômio de grau 
com coeficientes em 
.
Partiremos de (2) sem nenhuma hipótese adicional sobre 
e 
. O argumento nos conduzirá naturalmente à condição que 
deve satisfazer para possuir exatamente 
algarismos na base 
. Não será necessário exibirmos as divisões em escada, pois cada divisão por 
resultará de uma aplicação da igualdade (2). Manipularemos um sistema de igualdades visando terminar com uma expressão polinomial apropriada para 
. Durante o processo, usaremos a seguinte propriedade da função piso (válida para quaisquer 
e 
inteiro positivo):
Iniciando o processo
Iniciamos o processo aplicando (2) à divisão de 
por 
. Então, por causa de (3),
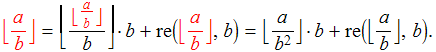
Quando levamos essa expressão para 
na igualdade (2) e desenvolvemos os produtos, descobrimos que
que também é uma expressão polinomial em 
— desta vez, de grau 
. Uma nova aplicação de (2) e (3) nos dá
que substituída em (4) nos leva a
Paremos para observar o que fizemos até agora:
Deve estar claro que se repetirmos o procedimento 
vezes, teremos algo como
ou ainda
Exercício 1
Prove (6) por indução em m.
O ponto de parada
Que valor de 
terminará o processo? Naturalmente, queremos que 
seja o primeiro (o menor) número 
tal que
pois com isso temos pelo menos a certeza de que todos os coeficientes do polinômio (6) ficarão no conjunto 
. Ora (lembrando que 
),
Portanto, 
será o menor 
que satisfaz (7) se, e somente se, cumprir as duas condições seguintes:
(A) 
;
(B) 
.
(Isso resulta da própria definição de menor. Veja o artigo Teoria da Ordem (Parte II) em Conceitos Fundamentais, neste site.)
De (B) concluímos que 
. Juntamente com a condição (A), isto nos dá
que é exatamente a condição que havíamos imposto ao número 
para que tivesse 
algarismos na base 
.
O leitor não terá dificuldade em ver que (8) é equivalente a
(A propósito, isso foi provado no Capítulo IX do CD Números — link Característica e Mantissa de um Logaritmo.)
Exercício 2
Mostre que se 
satisfaz as condições (A) e (B) acima, então 
. Isto garante que (6), como um polinômio em 
, tem grau 
. Em termos da divisão em escada mencionada na introdução, isto significa que o último resto (
) é 
.
O resultado final
Com base em (9) e (6), podemos dizer que
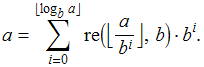
Eis aí, finalmente, a gloriosa representação posicional de 
na base 
, numa forma explícita. Podemos ver que o 
-ésimo algarismo de 
na base 
é
(contado da esquerda para a direita na disposição tradicional).
Algarismos para todos os números
O que acontece se não tivermos 
? Ora, segue-se da discussão acima que sempre podemos encontrar um 
nessas condições. De fato, 
A partir daí podemos invocar o resultado que acabamos de provar e concluir que 
possui uma representação posicional na base 
.
Carlos César de Araújo, 15 de abril de 2006, 16:32:45