para todos os números naturais 
. Não menos importante é a unicidade dessa representação: a expressão
Unicidade
Matemática para Gregos & Troianos
Mostramos a existência de uma representação posicional na base para todos os números naturais . Não menos importante é a unicidade dessa representação: a expressão
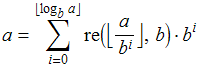
é a única maneira de representar 
como um polinômio em 
de grau 
com coeficientes em 
. Por outras palavras, se nos disserem que 
são números tais que
(1) 
;
(2) 
;
(3) 
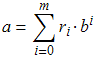
então estamos autorizados a concluir que 
e
para todo 
de 
a 
.
A unicidade da representação posicional pode ser provada de várias maneiras (com ou sem o uso explícito da função piso). O argumento mais comum consiste em aplicar repetidamente a unicidade do resto de uma divisão. Bem menos conhecido é o fato de que podemos nos valer da existência para provar a unicidade! É o que vamos mostrar agora. O raciocínio poderá parecer sofisticado, mas é muito simples e de largo emprego na matemática. Baseia-se no seguinte fato (que é essencialmente um teorema de Combinatória):
Teorema. Se 
e 
são conjuntos finitos com o mesmo número de elementos, então toda função sobrejetora 
é injetora.
(Para uma discussão mais detalhada, veja o artigo Funções na seção Conceitos Fundamentais deste site.)
Isso posto, fixe um número natural 
e considere a função 
com as seguintes especificações:
• 
é o conjunto das 
-uplas 
de elementos do conjunto 
tais que 
. (Ou seja, o primeiro elemento deve ser diferente de zero.) Em termos de produtos cartesianos, 
.
• 
é o conjunto dos naturais de 
até 
.
• 
.
Pode-se constatar facilmente o seguinte com relação a esses dados:
• O conjunto 
possui 
elementos.
• O conjunto 
possui 
elementos.
• A função 
é sobrejetora. De fato, foi precisamente isto que provamos nas duas páginas anteriores.
Segue-se do Teorema acima que a função 
é injetora. Isto significa que se
então
Ou ainda: se duas representações de mesmo grau na base 
, 
e 
, são iguais, então os algarismos correspondentes são iguais.
Conforme dissemos no início deste artigo, quando as pessoas pensam em “números”, elas enxergam apenas uma representação particular dos mesmos, a saber, a escrita posicional na base 
. Mas são os teoremas de existência e unicidade que provamos aqui que garantem o “sucesso” dessa representação.
Carlos César de Araújo, 16 de abril de 2006, 17:57:26