Ensaiando estratégias

A resolução de uma equação simples como mostrou que pode haver mais de um caminho a seguir: a passagem do 7 para o segundo membro tanto pode ser obtida pela adição de 7 como pela subtração de . Com o playEquation, o estudante poderá desenvolver uma percepção mais aguçada do formalismo algébrico pela facilidade de ensaiar estratégias sem se fatigar com a reescrita das equações.

Como um exemplo mais interessante de equação que admite vários caminhos de resolução, tomemos a equação fracionária

(que já vem no caderno de exemplos).

Como primeiro passo para a resolução dessa equação, a maioria dos estudantes do Ensino Médio propõe que se adicionem as frações no primeiro membro. No playEquation, basta colocar o cursor em qualquer ponto da equação e clicar no botão . Eis o resultado:

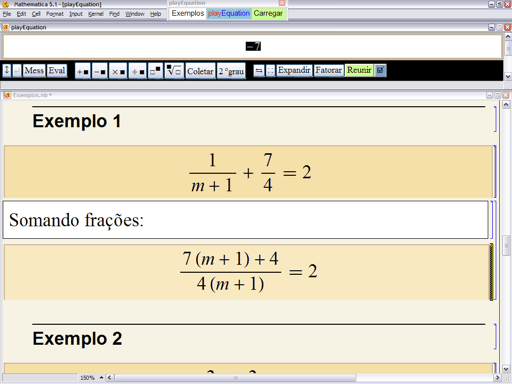
(Não é necessário selecionar, ou digitar uma expressão no campo de dados, neste caso, porque a operação aplicada pelo botão é não-paramétrica. Essa operação simplesmente “reúne” frações numa fração única, somando-as conforme a regra .)

Qual será o próximo passo? A resposta mais freqüente é: “multiplique cruzado”. Isto é, o estudante mentalmente enxerga a última igualdade como uma proporção cujo quarto termo é 1. Um sinal clássico para indicar proporção é ∷ (quatro pontos). No playEquation, a regra da “multiplicação cruzada” foi implementada no botão . Quando se clica neste botão, o programa apresenta rapidamente o seguinte

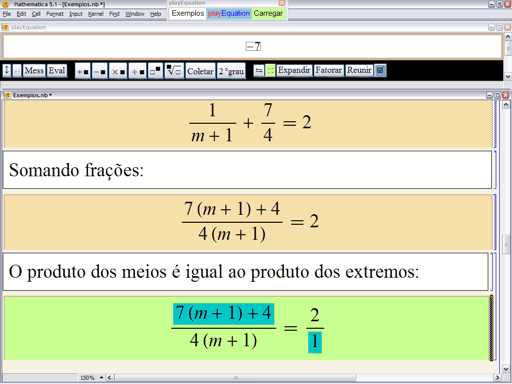
depois o seguinte

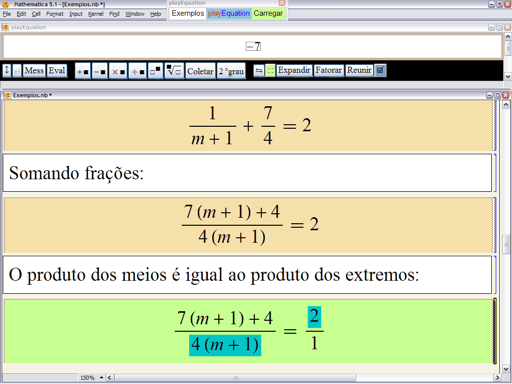
e então termina com

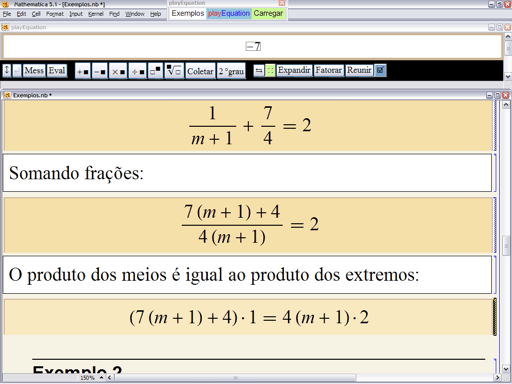
Neste ponto, todos concordam com a próxima ação: os produtos devem ser efetuados. No playEquation, basta clicar no botão , que expande ou desenvolve produtos e potências. Na tela abaixo apresentamos o resultado seguido de dois outros passos:

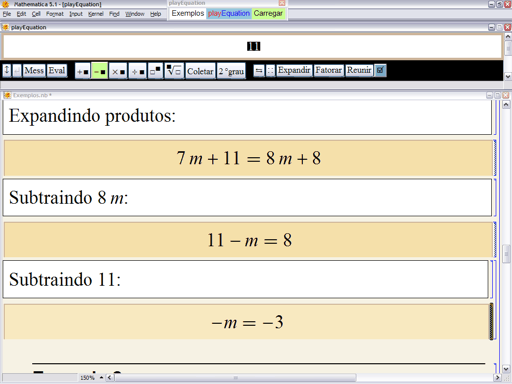
A equação está quase resolvida; resta multiplicar (ou dividir) os dois membros por . Como não aparece em nenhuma parte da equação, o usuário teria, em princípio, que entrar com no campo de dados e clicar no botão (multiplicar por ■). Contudo, o playEquation oferece um atalho para esta situação:

• selecione o sinal ;
• clique no botão (multiplicar por ■).

Feito isto, o número vai para o campo de dados e é aplicado à equação de acordo com a operação multiplicar por. Eis o resultado:

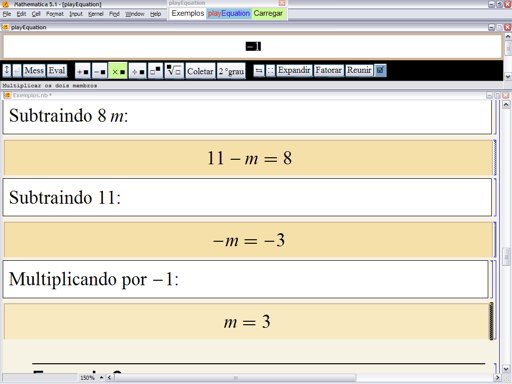
Acabamos de resolver a equação em 6 (seis) passos. Com o playEquation, o estudante terá a oportunidade de se exercitar rapidamente descobrindo outras rotas possíveis. Abaixo, mostramos uma solução que envolve apenas 3 (três) passos:

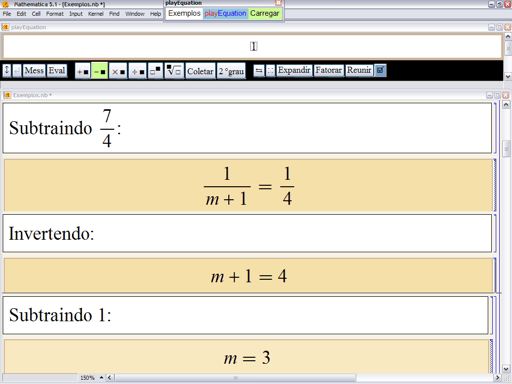
Como as frações foram invertidas? Na prática, invertemos uma fração simplesmente trocando seus termos de posição. Matematicamente, isto é o mesmo que elevar a fração ao expoente . Assim, para inverter uma fração no playEquation, basta colocar no campo de dados e clicar no botão (elevar ao expoente ■).