Teoria da Ordem
(Parte 1)
Carlos César de Araújo
 |
Introdução
Inúmeros conceitos matemáticos envolvem uma relação de ordem num conjunto. A divisão de polinômios depende de uma ordenação das variáveis. A matriz de um sistema de equações lineares depende da ordem das incógnitas. Operações básicas como a de formar uma união de conjuntos e calcular um máximo divisor comum, embora tão diferentes entre si, não só dependem de uma relação de ordem em seus respectivos domínios, como são, abstratamente falando, a “mesma” operação — oriunda dessas diferentes ordens. O primeiro dos 23 problemas de Hilbert menciona um fato sobre ordens (que logo depois se provaria ser equivalente ao Axioma da Escolha).
Relações de ordem surgem em incontáveis partes da Matemática, seja “elementar”, “avançada”, “pura” ou “aplicada”, tais como na Álgebra, Topologia, Lógica, Geometria, Física, Lingüística e Teoria da Programação. Vários artigos do Matemática para Gregos & Troianos tratam de assuntos que envolvem relações de ordem. Conseqüentemente, o que se ganha com o estudo geral dessas relações é o mesmo que se lucra com o de qualquer outra estrutura matemática abstrata: economia de raciocínio e clareza conceitual.
Este artigo apresenta a teoria da ordem princialmente como uma referência para outros artigos do site, nos quais aplicamos as definições e teoremas gerais aqui apresentados aos casos particulares de interesse. Por causa disso, a exposição aqui é mais concisa e formal do que de costume. (O artigo O Conceito de Estrutura serve de preparo para o leitor iniciante.) Muitas demonstrações foram deixadas para exame mais detalhado em outras seções do site (particularmente a seção Lógica). Além disso, este artigo estará em permanente expansão: definições e resultados serão inseridos em outras Partes de tempos em tempos, conforme a necessidade imposta por outros artigos.
Observações sobre notação e terminologia
Veremos diversos tipos de relações de ordem, cada um definido por uma lista de propriedades. A maioria dessas propriedades são formas “desencarnadas” das que valem para as familiares relações de desigualdade ![]() (
(![]() é menor ou igual a
é menor ou igual a ![]() ) e
) e ![]() (
(![]() é menor que
é menor que ![]() ) entre números. Na verdade, a teoria da ordem pode ser vista como um estudo puramente axiomático das desigualdades: simplesmente escolhemos certas propriedades e definições que envolvem essas relações, estendemo-las a conjuntos arbitrários e examinamos a força lógica das mesmas em conjunção com outras condições.
) entre números. Na verdade, a teoria da ordem pode ser vista como um estudo puramente axiomático das desigualdades: simplesmente escolhemos certas propriedades e definições que envolvem essas relações, estendemo-las a conjuntos arbitrários e examinamos a força lógica das mesmas em conjunção com outras condições.
Em cada definição ou axioma teremos sempre dois ingredientes básicos: um conjunto ![]() e uma relação binária
e uma relação binária ![]() em
em ![]() , isto é, uma relação que só pode vigorar entre dois elemento de cada vez. (Alternativamente, podemos olhar
, isto é, uma relação que só pode vigorar entre dois elemento de cada vez. (Alternativamente, podemos olhar ![]() como um conjunto de pares ordenados e dizer que
como um conjunto de pares ordenados e dizer que ![]() .) O mesmo adjetivo usado para uma ordem
.) O mesmo adjetivo usado para uma ordem ![]() também é aplicado à estrutura
também é aplicado à estrutura ![]() . Por exemplo, as sentenças “
. Por exemplo, as sentenças “![]() é uma ordem parcial em
é uma ordem parcial em ![]() ” e “
” e “![]() é um conjunto parcialmente ordenado” são tomadas como sinônimas.
é um conjunto parcialmente ordenado” são tomadas como sinônimas.
Uma parte substancial dos teoremas (conseqüências dos axiomas e definições) pode ser obtida por manipulação mecânica de conectivos e quantificadores — não passando, portanto, de um puro exercício de Lógica. Visando ressaltar a importância desse fato, usamos livremente símbolos lógicos como ![]() (“e”),
(“e”), ![]() (“ou”),
(“ou”), ![]() (“se-então”),
(“se-então”), ![]() (“se e somente se”),
(“se e somente se”), ![]() (“para todo”) e
(“para todo”) e ![]() (“existe”). Para reduzir o comprimento dos enunciados, omitimos a referência ao conjunto
(“existe”). Para reduzir o comprimento dos enunciados, omitimos a referência ao conjunto ![]() na maioria dos quantificadores. Assim, conforme o contexto, uma sentença da forma
na maioria dos quantificadores. Assim, conforme o contexto, uma sentença da forma ![]() significará
significará ![]() . (Analogamente, sentenças sem quantificadores em definições e teoremas devem ser entendidas como estando precedidas de quantificadores universais para cada variável livre.)
. (Analogamente, sentenças sem quantificadores em definições e teoremas devem ser entendidas como estando precedidas de quantificadores universais para cada variável livre.)
Se ![]() , então o fato de
, então o fato de ![]() estar na relação
estar na relação ![]() com
com ![]() pode ser expresso por
pode ser expresso por ![]() (notação prefixa) ou
(notação prefixa) ou ![]() (notação infixa). Em se tratando de relações de ordem, são comuns duas convenções: uso da notação infixa e dos símbolos tradicionais
(notação infixa). Em se tratando de relações de ordem, são comuns duas convenções: uso da notação infixa e dos símbolos tradicionais ![]() e
e ![]() para designar ordens em geral. (São também freqüentes o uso de variantes estilísticas de
para designar ordens em geral. (São também freqüentes o uso de variantes estilísticas de ![]() , tais como
, tais como ![]() e
e ![]() .) Também usaremos sinais infixos, mas seguiremos uma prática mais recente (e comum entre os cientistas da computação) que consiste em usar os símbolos “quadrados”
.) Também usaremos sinais infixos, mas seguiremos uma prática mais recente (e comum entre os cientistas da computação) que consiste em usar os símbolos “quadrados” ![]() e
e ![]() como variáveis para ordens. As relações inversas são designadas por
como variáveis para ordens. As relações inversas são designadas por ![]() e
e ![]() , respectivamente. Lembramos que a inversa (ou oposta) de uma relação
, respectivamente. Lembramos que a inversa (ou oposta) de uma relação ![]() é a relação
é a relação ![]() que vale entre
que vale entre ![]() e
e ![]() se, e somente se,
se, e somente se, ![]() . Assim, por definição, teremos sempre
. Assim, por definição, teremos sempre
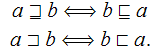
Na teoria da ordem, é útil dispor de maneiras alternativas de expressar em palavras uma afirmação da forma ![]() (além da tradicional “
(além da tradicional “![]() está na relação
está na relação ![]() com
com ![]() ”). Citamos abaixo alguns exemplos:
”). Citamos abaixo alguns exemplos:
• ![]() é
é ![]() -antecessor de
-antecessor de ![]()
• ![]() é
é ![]() -subordinado a
-subordinado a ![]()
• ![]() é
é ![]() -sucessor de
-sucessor de ![]()
• ![]()
![]() -domina
-domina ![]() .
.
Na prática, é muitas vezes possível omitir a referência explícita a ![]() sem causar ambigüidades (o que é feito, aliás, em quase toda a literatura).
sem causar ambigüidades (o que é feito, aliás, em quase toda a literatura).
Outras definições e convenções notacionais (que não são exclusivas das relações de ordem) são:
• ![]() com uma extensão óbvia (usando indução finita) para qualquer número finito de elementos:
com uma extensão óbvia (usando indução finita) para qualquer número finito de elementos: ![]()
• ![]() . Chamamos
. Chamamos ![]() a relação estrita derivada de
a relação estrita derivada de ![]() .
.
• ![]() , com extensões análogas para um número finito qualquer de elementos.
, com extensões análogas para um número finito qualquer de elementos.
Uma conseqüência da definição de ![]() é que
é que
![]()
Este é um exemplo de conseqüência “puramente lógica” de definições (depende apenas da semântica dos sinais lógicos e da relação de igualdade).
Finalmente, às vezes achamos útil usar o símbolo ![]() como uma maneira sucinta de declarar que se tem uma igualdade aceita por definição (e não como conseqüência de algum fato prévio).
como uma maneira sucinta de declarar que se tem uma igualdade aceita por definição (e não como conseqüência de algum fato prévio).
Pré-ordens
Muitos autores iniciam a teoria da ordem com as pré-ordens, mas rapidamente desenvolvem a maioria das definições (como as de mínimo e supremo) para as ordens parciais (assunto da Parte 2). Contudo, veremos que é útil explorar as pré-ordens ao máximo (!) — até que o esgotamento de resultados interessantes nos force a impor mais restrições.
Um conjunto pré-ordenado é um par ![]() , onde
, onde ![]() é uma relação em
é uma relação em ![]() que é reflexiva e transitiva, isto é, que satisfaz as seguintes condições:
que é reflexiva e transitiva, isto é, que satisfaz as seguintes condições:

Recordamos que uma relação de equivalência em ![]() é uma relação reflexiva, transitiva e simétrica. Portanto, pré-ordens são uma generalização das relações de equivalência. Uma propriedade que muito facilita o estudo das ordens é a anti-simetria, isto é, o fato de
é uma relação reflexiva, transitiva e simétrica. Portanto, pré-ordens são uma generalização das relações de equivalência. Uma propriedade que muito facilita o estudo das ordens é a anti-simetria, isto é, o fato de ![]() sempre implicar
sempre implicar ![]() . Ela vale (por definição) para as ordens parciais que mencionamos há pouco. Contudo, muitas pré-ordens interessantes não são anti-simétricas, como é o caso da relação
. Ela vale (por definição) para as ordens parciais que mencionamos há pouco. Contudo, muitas pré-ordens interessantes não são anti-simétricas, como é o caso da relação ![]() (
(![]() divide
divide ![]() ) num anel comutativo (sobre a qual falaremos em outro artigo). Mas ainda que a relação
) num anel comutativo (sobre a qual falaremos em outro artigo). Mas ainda que a relação ![]() não seja necessariamente a igualdade, tem em comum com ela o fato de ser uma relação de equivalência, conforme veremos agora.
não seja necessariamente a igualdade, tem em comum com ela o fato de ser uma relação de equivalência, conforme veremos agora.
Definição. ![]() .
.
Teorema 1. Se ![]() é uma pré-ordem em
é uma pré-ordem em ![]() , então
, então ![]() é uma relação de equivalência em
é uma relação de equivalência em ![]() .
.
Demonstração.
A relação estrita ![]() derivada de uma pré-ordem
derivada de uma pré-ordem ![]() jamais é uma pré-ordem, pois não é reflexiva. Mas pode ser transitiva, se bem que não necessariamente. É fácil ver que de
jamais é uma pré-ordem, pois não é reflexiva. Mas pode ser transitiva, se bem que não necessariamente. É fácil ver que de ![]() podemos concluir que
podemos concluir que ![]() e
e ![]() ; mas como a relação
; mas como a relação ![]() não é transitiva, não podemos asserir que
não é transitiva, não podemos asserir que ![]() e
e ![]() . Contra-exemplos concretos serão vistos em outra parte.
. Contra-exemplos concretos serão vistos em outra parte.
Dualidade
Veremos que várias proposições sobre uma pré-ordem ![]() valem também para a relação inversa
valem também para a relação inversa ![]() . O teorema abaixo mostra que a inversa de uma pré-ordem também é uma pré-ordem.
. O teorema abaixo mostra que a inversa de uma pré-ordem também é uma pré-ordem.
Teorema 2. ![]() é uma pré-ordem em
é uma pré-ordem em ![]() se, e somente se,
se, e somente se, ![]() é uma pré-ordem em
é uma pré-ordem em ![]() .
.
Realmente, dada uma relação (binária) ![]() , é fácil ver que
, é fácil ver que ![]() é reflexiva se, e somente se,
é reflexiva se, e somente se, ![]() é reflexiva. Do mesmo modo, as sentenças “
é reflexiva. Do mesmo modo, as sentenças “![]() é transitiva” e “
é transitiva” e “![]() é transitiva” são sinônimas. (Veja as provas na seção Lógica.) O Teorema 2 simplesmente exprime esses dois fatos numa outra terminologia.
é transitiva” são sinônimas. (Veja as provas na seção Lógica.) O Teorema 2 simplesmente exprime esses dois fatos numa outra terminologia.
Seja ![]() uma afirmação qualquer (definição ou teorema) envolvendo uma pré-ordem
uma afirmação qualquer (definição ou teorema) envolvendo uma pré-ordem ![]() num conjunto
num conjunto ![]() . A proposição dual de
. A proposição dual de ![]() é a proposição
é a proposição ![]() que se obtém de
que se obtém de ![]() substituindo a relação
substituindo a relação ![]() pela sua inversa
pela sua inversa ![]() . Em particular, o dual de um conceito definido em
. Em particular, o dual de um conceito definido em ![]() é o conceito correspondente definido em
é o conceito correspondente definido em ![]() . Isso será esclarecido adiante.
. Isso será esclarecido adiante.
Decorre do Teorema 2 que se ![]() é conseqüência lógica das condições (O1) e (O2), então
é conseqüência lógica das condições (O1) e (O2), então ![]() também o é. Desse modo, se num teorema válido para conjuntos pré-ordenados trocarmos cada conceito pelo seu dual, o resultado é ainda um teorema válido para conjuntos pré-ordenados. É evidente a importância prática desse resultado: cada teorema automaticamente nos presenteia com o seu dual.
também o é. Desse modo, se num teorema válido para conjuntos pré-ordenados trocarmos cada conceito pelo seu dual, o resultado é ainda um teorema válido para conjuntos pré-ordenados. É evidente a importância prática desse resultado: cada teorema automaticamente nos presenteia com o seu dual.
Exemplos
Por ora, mencionaremos rapidamente apenas três exemplos simples de pré-ordem. O exemplo dos anéis será explorado detalhadamente em outro lugar.
Os conjuntos numéricos fundamentais ![]() ,
, ![]() ,
, ![]() e
e ![]() são pré-ordenados pela relação
são pré-ordenados pela relação ![]() (menor ou igual a).
(menor ou igual a).
Qualquer coleção ![]() de conjuntos é pré-ordenada pela relação de inclusão, aqui denotada por
de conjuntos é pré-ordenada pela relação de inclusão, aqui denotada por ![]() . Ou seja,
. Ou seja, ![]() , com
, com ![]() , é um conjunto pré-ordenado. Lembramos que a relação
, é um conjunto pré-ordenado. Lembramos que a relação ![]() entre conjuntos é definida por
entre conjuntos é definida por
![]()
Há autores que denotam a inclusão por ![]() , deixando o símbolo
, deixando o símbolo ![]() para a relação estrita (isto é,
para a relação estrita (isto é, ![]() ). Esse esquema tem as suas vantagens, mas não o adotaremos neste artigo.
). Esse esquema tem as suas vantagens, mas não o adotaremos neste artigo.
Finalmente, qualquer anel com unidade ![]() é pré-ordenado pela relação
é pré-ordenado pela relação ![]() (lê-se “
(lê-se “![]() divide
divide ![]() ”), definida por
”), definida por ![]() . (A existência de unidade garante a reflexividade; e a transitividade decorre da associatividade da multiplicação do anel.)
. (A existência de unidade garante a reflexividade; e a transitividade decorre da associatividade da multiplicação do anel.)
Intervalos
Dados uma pré-ordem ![]() em
em ![]() e um elemento
e um elemento ![]() , o conjunto dos sucessores de
, o conjunto dos sucessores de ![]()
![]()
(que é a imagem de ![]() pela relação
pela relação ![]() ) é um exemplo de intervalo em
) é um exemplo de intervalo em ![]() . Mostramos abaixo algumas notações para esse intervalo que se encontram na literatura:
. Mostramos abaixo algumas notações para esse intervalo que se encontram na literatura:
![]()
Note-se que o intervalo depende da relação ![]() , embora isso não seja ressaltado por nenhuma dessas notações. Neste artigo usaremos a primeira notação. Quando quisermos tornar explícita a relação
, embora isso não seja ressaltado por nenhuma dessas notações. Neste artigo usaremos a primeira notação. Quando quisermos tornar explícita a relação ![]() , escreveremos
, escreveremos
![]()
Por dualidade (isto é, aplicando essa definição à pré-ordem inversa), obtemos o intervalo “à direita”
![]()
ou seja,
![]()
Outras espécies de intervalo em ![]() são definidas abaixo:
são definidas abaixo:
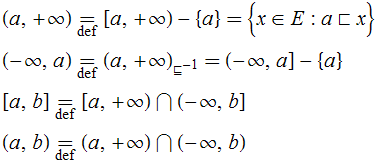
(Usamos essas notações clássicas como uma concessão à tradição. Por ora, os sinais “![]() ” e “
” e “![]() ” não passam de meras decorações notacionais.)
” não passam de meras decorações notacionais.)
É fácil e instrutivo formular os axiomas de pré-ordem em termos de intervalos. Temos (onde deixamos implícita a referência a ![]() ):
):
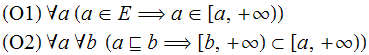
A condição de transitividade (O2) também pode ser escrita em termos de intervalos “à direita”:
![]()
Teorema 3. Se ![]() é uma pré-ordem em
é uma pré-ordem em ![]() , então
, então
![]()
Corolário. Se ![]() é uma pré-ordem em
é uma pré-ordem em ![]() , então
, então
![]()
Com as formulações dos axiomas em termos de intervalos, tanto o Teorema 3 como o seu corolário tornam-se evidentes. O corolário resulta da anti-simetria da inclusão (se ![]() e
e ![]() , então
, então ![]() ), e deixa mais claro porque a relação
), e deixa mais claro porque a relação ![]() é de equivalência (Teorema 1).
é de equivalência (Teorema 1).
Majorantes e Minorantes
Doravante, até o final deste artigo, fixaremos um conjunto pré-ordenado ![]() e um conjunto
e um conjunto ![]() .
.
Diz-se que ![]() é um majorante de
é um majorante de ![]() quando satisfaz uma qualquer das seguintes condições equivalentes:
quando satisfaz uma qualquer das seguintes condições equivalentes:
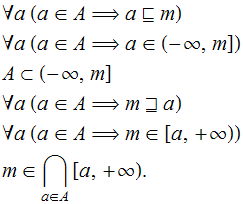
Ou seja, um majorante de ![]() é um elemento que domina todos os elementos de
é um elemento que domina todos os elementos de ![]() .
.
Não há uma notação padrão para o conjunto dos majorantes de ![]() , mas a última condição acima mostra que podemos exprimi-lo como uma interseção de intervalos “à esquerda”. Se o denotarmos por
, mas a última condição acima mostra que podemos exprimi-lo como uma interseção de intervalos “à esquerda”. Se o denotarmos por ![]() (sem referência à pré-ordem usada), então teremos a igualdade
(sem referência à pré-ordem usada), então teremos a igualdade
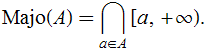
O dual de “majorante” é minorante. Assim, definimos um minorante de ![]() (com respeito a
(com respeito a ![]() ) como um
) como um ![]() que é majorante de
que é majorante de ![]() sob a pré-ordem oposta. Qualquer uma das cinco sentenças abaixo traduz essa condição:
sob a pré-ordem oposta. Qualquer uma das cinco sentenças abaixo traduz essa condição:
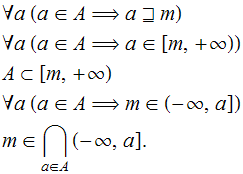
Portanto, se denotarmos o conjunto dos minorantes de ![]() por
por ![]() , então
, então
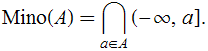
(Se insistíssemos em usar notações ultraprecisas, teríamos dito que ![]() .)
.)
Outra formulação da definição de majorante é a que decorre da equivalência (provada na seção Lógica)
![]()
(Em palavras: ![]() está contido em todo conjunto de
está contido em todo conjunto de ![]() se, e só se,
se, e só se, ![]() está contido na interseção desses conjuntos. Voltaremos a esse fato na Parte 2.) Isso posto, retomemos a definição de “
está contido na interseção desses conjuntos. Voltaremos a esse fato na Parte 2.) Isso posto, retomemos a definição de “![]() ”:
”: ![]() Após usarmos intervalos como no Teorema 3, obtemos as seguintes condições equivalentes à de majorante de
Após usarmos intervalos como no Teorema 3, obtemos as seguintes condições equivalentes à de majorante de ![]() :
:
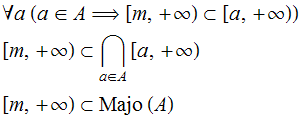
Analogamente, cada uma das duas condições abaixo diz o mesmo que “![]() é minorante de
é minorante de ![]() ”:
”:
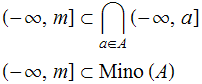
Como exercício, deixamos para o leitor verificar que
![]()
Maxímos e Mínimos
Dando prosseguimento à discussão anterior, dizemos que ![]() é um máximo de
é um máximo de ![]() quando é um elemento de
quando é um elemento de ![]() que é também majorante de
que é também majorante de ![]() . Assim, a condição de máximo é a conjunção das duas seguintes:
. Assim, a condição de máximo é a conjunção das duas seguintes:
• ![]() ;
;
• ![]() é majorante de
é majorante de ![]() :
: ![]() .
.
Dualmente, dizemos que ![]() é um mínimo de
é um mínimo de ![]() quando
quando
• ![]() ;
;
• ![]() é minorante de
é minorante de ![]() :
: ![]() .
.
Portanto, o conjunto dos máximos de ![]() é
é
![]()
e o conjunto dos mínimos de ![]() é
é
![]()
Na ausência de condições adicionais sobre a pré-ordem ![]() , é impossível concluir que dois elementos máximos (ou mínimos) são iguais. A relação mais geral entre dois elementos máximos é a seguinte:
, é impossível concluir que dois elementos máximos (ou mínimos) são iguais. A relação mais geral entre dois elementos máximos é a seguinte:
Teorema 4. ![]() .
.
A comprovação é imediata, valendo o mesmo para mínimos (por dualidade).
Supremos e Ínfimos
Das definições anteriores vê-se facilmente o seguinte: se ![]() é majorante de
é majorante de ![]() e
e ![]() , então
, então ![]() também é majorante de
também é majorante de ![]() . Ou seja, “acima” de um majorante temos mais majorantes. Assim, torna-se interessante examinar majorantes que sejam mínimos. Isto nos leva à importante noção de “supremo”. Dualizando a discussão, teremos o conceito de “ínfimo”.
. Ou seja, “acima” de um majorante temos mais majorantes. Assim, torna-se interessante examinar majorantes que sejam mínimos. Isto nos leva à importante noção de “supremo”. Dualizando a discussão, teremos o conceito de “ínfimo”.
Diz-se que ![]() é um supremo de
é um supremo de ![]() quando são verdadeiras as duas afirmações seguintes:
quando são verdadeiras as duas afirmações seguintes:
(1) ![]() é um majorante de
é um majorante de ![]() ;
;
(2) ![]() é um minorante dos majorantes de
é um minorante dos majorantes de ![]() .
.
Ou seja, se designarmos o conjunto dos supremos de ![]() por
por ![]() , então, por definição,
, então, por definição,
![]()
O teorema seguinte nos dá uma caracterização do supremo que será de enorme importância.
Teorema 5. ![]()
Demonstração.
Corolário. 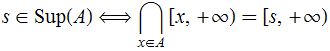 .
.
Conforme antecipamos, o dual de “supremo” é “ínfimo”. Contudo, é pedagogicamente mais útil definir “ínfimo” separadamente e depois provar a dualidade. Assim, dizemos que ![]() é um ínfimo de
é um ínfimo de ![]() quando:
quando:
(1) ![]() é um minorante de
é um minorante de ![]() ;
;
(2) ![]() é um majorante dos minorantes de
é um majorante dos minorantes de ![]() .
.
Escrevamos ![]() para o conjunto dos ínfimos. Então, a definição de ínfimo assume o seguinte aspecto:
para o conjunto dos ínfimos. Então, a definição de ínfimo assume o seguinte aspecto:
![]()
Temos, agora, a esperada dualidade (com o devido destaque para a relação ![]() ):
):
Teorema 6. ![]() .
.
Demonstração.
Corolário. 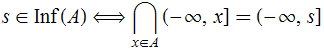 .
.
Demonstração.
Teorema 7. ![]() .
.
Demonstração.
Corolário. ![]() .
.
Continua.
Bibliografia
Carlos César de Araújo, 18 de novembro de 2006, 15:36:55