Cramer e Sarrus no Mathematica
Implementação

Esta página contém uma breve descrição das estratégias empregadas na programação do CramerSarrus. Embora seja endereçada a usuários avançados do Mathematica, algumas passagens podem esclarecer e mencionar detalhes relevantes que omitimos da apresentação anterior.

Como já vimos, uma vez escrita uma expressão matemática, o uso do CramerSarrus envolve apenas dois passos:

Passo 1: o usuário coloca o cursor em qualquer ponto da expressão;
Passo 2: o usuário clica num botão apropriado da paleta CramerSarrus.

As expressões matemáticas de interesse são dos seguintes tipos:

• um sistema linear (com ou sem chave à esquerda). Botão a ser clicado: .
• uma matriz . Botão a ser clicado: .
• uma matriz ou determinante . Botão a ser clicado: ou .
• uma matriz, submatriz ou determinante . Botão a ser clicado: .

Todas essas expressões devem ser escritas em notação matemática tradicional, exatamente como nos exemplos apresentados. É importante salientar este fato porque o Mathematica reconhece expressões em diferentes formatos. Por exemplo, sistemas de equações e matrizes podem ser especificados simplesmente como listas (expressões com Head igual a List, também escritas com seus elementos entre chaves). Assim, um sistema linear pode ser dado como uma lista de equações lineares com incógnitas. Internamente, uma matriz numérica é uma lista com listas (as linhas da matriz) de comprimento . (Matematicamente, isso corresponde à idéia de que uma funcão “equivale” a uma função de no conjunto das funções de em .)

Dado o fim educacional do CramerSarrus, essas representações em termos de listas não serão reconhecidas pelos algoritmos implementados no pacote (embora seja fácil providenciar tal extensão).

Seleção e Captura de Notações

No Mathematica, toda expressão simbólica possui uma representação textual que codifica sua forma visual. Esse “código tipográfico”  determina a apresentação da expressão, a sua “aparência” na tela — independentemente da sua semântica ou interpretação. Em particular, notações estritamente bidimensionais (como a apresentação de matrizes por grades delimitadas por parênteses) são definidas por configurações de caixas tipográficas (objetos Box). A idéia de codificar notações é tão natural quanto a de codificar objetos de desenho, e está presente em linguagens de marcação como o e o MathML. (Diga-se de passagem que a arquitetura dos elementos de apresentação do MathML deriva da que é usada no Mathematica.)

Numa sessão normal do Mathematica, não temos que lidar com representações textuais diretamente porque o kernel cuida automaticamente das mesmas durante a avaliação (processamento) das expressões. (A avaliação se dá, por exemplo, quando o usuário pressiona a tecla Enter do teclado numérico.) No CramerSarrus, porém, a avaliação é disparada via botões externos ao caderno do usuário. O principal elemento de um botão é a opção ButtonFunction, que roda um algoritmo quando o botão é clicado.

No CramerSarrus, quando o usuário clica num dos quatro botões acima, o front end expande progressivamente a seleção (usando While e NotebookRead) enquanto examina a representação textual da expressão à procura do padrão (pattern) tipográfico apropriado. Por exemplo, o padrão

com

descreve a representação textual de uma grade de equações (que corresponde a um sistema) ou de uma matriz em notação tradicional, possivelmente com estilos. Em particular, matrizes e determinantes são identificados por expressões da forma

onde

Os objetos StyleBox assinalam alterações de estilo tais como cor, tamanho, fonte etc.

Se o padrão esperado não for detectado durante um ciclo, o CramerSarrus abre uma janela (na verdade, um objeto Notebook) com uma mensagem para o usuário — que deve, então, tentar novamente (talvez reposicionando o cursor na expressão ou usando o botão correto).

Interpretação e Processamento

Além de uma representação textual, uma notação matemática possui também uma interpretação (ou conteúdo, na terminologia da MathML). O Mathematica possui um banco padrão de regras que associam um significado a cada representação textual. Essas regras podem ser modificadas caso se queira definir notações especiais. O leitor avançado certamente conhece o pacote Notation, criado por Jason Harris para automatizar essa tarefa. Entretanto, nenhum recurso do pacote Notation é utilizado no CramerSarrus.

No CramerSarrus, feita a captura da representação textual com a seleção progressiva, entram em cena as funções ToExpression e MakeExpression, que convertem as caixas tipográficas nos objetos matemáticos correspondentes (matrizes ou sistemas de equações). Vejamos o caso do botão . Uma vez convertido um sistema de equações numa lista de equações, temos que extrair as matrizes dos coeficientes e dos termos independentes do sistema (relativamente às incógnitas escolhidas pelo usuário na paleta de abertura). A partir do Mathematica 5.0, essas matrizes se extraem facilmente com a função CoefficientArrays. No caso do botão , o processamento semântico envolve a extração das submatrizes complementares (desta vez usando Part e Drop) de cada elemento da linha ou coluna especificadas pelo usuário. (Para cuidar do teorema geral de Laplace, a ser apresentado na próxima versão do pacote, usamos apenas Part.)

Formatação e Exibição

Após a realização dos cálculos, é preciso apresentar os resultados novamente em notação bidimensional na tela do usuário. (Além disso, essa “notação de saída” pode ou não ser consistente com a “notação de entrada”.) Note-se, por exemplo, que o CramerSarrus apresenta a regra de Cramer como uma seqüência de quocientes indicados (não efetuados) de determinantes, em cujos numeradores se destacam a coluna das constantes. A apresentação do desenvolvimento por cofatores (botão ) é ainda mais complexa, pois envolve a exibição de uma soma de produtos nos quais participam elementos decorados, potências não efetuadas e determinantes em notação tradicional.

A formatação dos resultados para apresentação se consegue basicamente com as funções ToBoxes e MakeBoxes atuando em TraditionalForm, mas com algumas alterações nas caixas resultantes — tais como a inserção de RowBox e FractionBox, ajustes nas opções de espaçamento das GridBox, ocultação de expressões por meio de StyleBox etc. A exibição final no caderno do usuário é feita com NotebookWrite.

Elementos da Interface

Como tudo no Mathematica, os botões, sons, janelas e paletas gerados pelo CramerSarrus são expressões normais da linguagem, regidas pela mesma sintaxe abstrata e sujeitas às mesmas manipulações estruturais (Map, MapThread etc) usadas para processar listas. Por exemplo, as paletas geradas pelos botões e são objetos Notebook (cadernos) cuja estrutura deve ser cuidadosamente montada como uma matriz (!) de botões (objetos ButtonBox) envolvida numa GridBox — que por sua vez comporá uma célula num caderno com opções especiais (dando-lhe a aparência de uma paleta flutuante). Desse modo, os mesmos elementos GridBox que formatam matrizes também sustentam grades de botões em paletas!

Os sons gerados pelo pacote foram criados com a função Play, mas, por razões de eficiência, essa função não participa diretamente do código-fonte do CramerSarrus. Em vez disso, a codificação em PostScript dos objetos Sound (gerados com Play) foi previamente armazenada em células ocultas para reprodução sonora quando necessário. (Para isso, a célula é localizada com NotebookFind e o som é reproduzido invocando-se FrontEndExecute.)

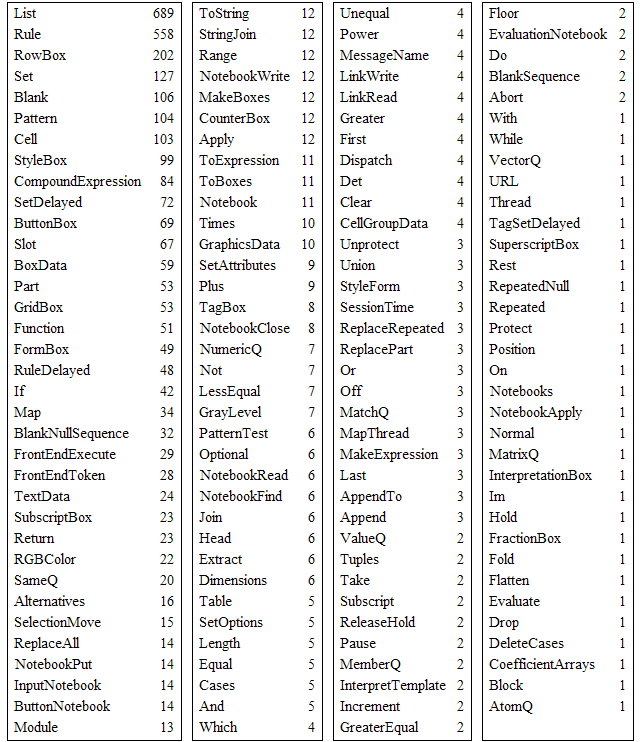
Funções Utilizadas

O código-fonte do CramerSarrus utilizou um total de 139 (cento e trinta e nove) funções do Mathematica. Esse número não inclui os nomes das diversas opções usadas em 26 (vinte e seis) dessas funções. Apresentamos abaixo uma tabela com os nomes das funções usadas juntamente com suas respectivas freqüências de ocorrência no código-fonte.

Criptografia

O código-fonte do CramerSarrus foi criptografado com a função Encode do Mathematica.

Carlos César de Araújo, 10 de novembro de 2006, 19:22:01