O pacote CramerSarrus — Sarrus e Laplace

Nesta versão, a paleta do CramerSarrus apresenta dois novos botões:

• O botão mostra o cálculo, passo a passo, de um determinante usando uma versão rápida da regra de Sarrus: os termos do determinante são extraídos sem que seja necessário repetir as duas primeiras colunas (como na versão tradicional da regra). Usando o CramerSarrus, o usuário não terá dificuldades para entender esse novo esquema.

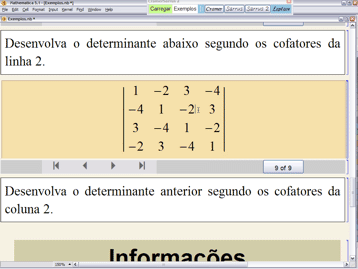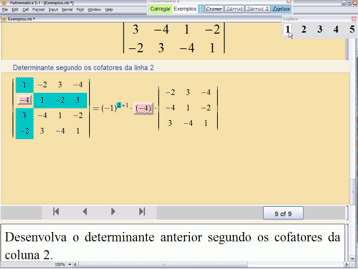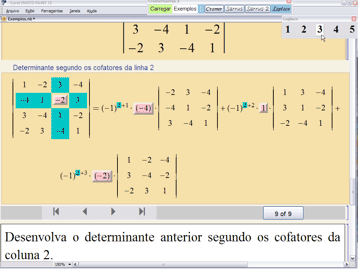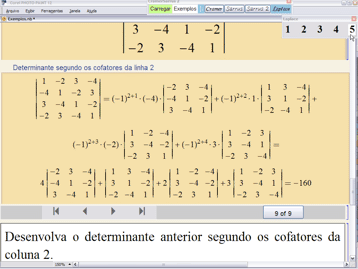
• O botão ensina como calcular um determinante qualquer somando os produtos dos elementos de uma linha (ou coluna) pelos seus cofatores. Essa expansão por cofatores é um caso particular de um resultado mais geral devido a Laplace (1749-1827). O Teorema de Laplace afirma que, para todo , o determinante de uma matriz é a soma dos produtos dos menores de linhas (ou colunas) pelos seus complementos algébricos. O cálculo por cofatores corresponde ao caso em que . Esse teorema geral de Laplace será implementado na versão 3 do CramerSarrus.

Carlos César de Araújo, 8 de novembro de 2006, 21:18:45